Für eine Menge ![]() bezeichne
bezeichne
![]() die Menge aller Funktionen von
die Menge aller Funktionen von ![]() nach
nach
![]() .
.
Für eine Menge ![]() bezeichne
bezeichne
![]() die Menge aller Funktionen von
die Menge aller Funktionen von ![]() nach
nach
![]() .
.
Eine Abbildung
Die Abbildungswerte ![]() heißen Folgenglieder,
und man schreibt
heißen Folgenglieder,
und man schreibt
Bemerkung.
Wenn ![]() eine Folge von Funktionen in
eine Folge von Funktionen in
![]() ist, so bilden für jedes
ist, so bilden für jedes ![]() die Funktionswerte eine
Folge
die Funktionswerte eine
Folge
![]() reeller Zahlen.
reeller Zahlen.
Eine Funktionenfolge ![]() in
in
![]() konvergiert punktweise auf
konvergiert punktweise auf
![]() gegen
gegen
![]() , falls für alle
, falls für alle ![]()
Bemerkung. Wenn eine Funktionenfolge ![]() für alle
für alle
![]() einen Grenzwert in
einen Grenzwert in
![]() hat, so definiert dies eine
Funktion
hat, so definiert dies eine
Funktion
![]() durch
durch
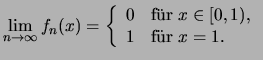
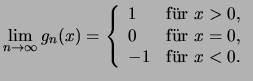
![$ h_n(x) = \left\{\begin{array}{ll}
nx& \text{f\uml ur \( x\in[0,\frac{1}{n}] \)...
...= 0 \).}\\
0& \text{f\uml ur \( x\in(\frac{2}{n},1] \).}
\end{array} \right. $](img2028.png)
Bemerkung. Es stellt sich die Frage, welche Eigenschaften der Glieder einer konvergenten Funktionenfolge sich auf die Grenzfunktion übertragen.
Die Beispiele (1.) und (2.) zeigen, daß bei punktweiser Konvergenz die Stetigkeit sich nicht auf die Grenzfunktion vererbt.
Wir müssen den Konvergenzbegriff für Funktionenfolgen verschärfen, um aus Eigenschaften der Folgenglieder auf entsprechende Eigenschaften der Grenzfunktion schließen zu können.
Im Beispiel (3.) konvergiert die Folge ![]() zwar punktweise
gegen die konstante Funktion
zwar punktweise
gegen die konstante Funktion ![]() , aber die
, aber die ![]() sind
offensichtlich keine gute Approximation der Grenzfunktion.
sind
offensichtlich keine gute Approximation der Grenzfunktion.
Noch krasser ist das Beispiel
![]() .
.
Eine Funktionenfolge ![]() in
in
![]() konvergiert gleichmäßig auf
konvergiert gleichmäßig auf ![]() gegen
eine Grenzfunktion
gegen
eine Grenzfunktion
![]() , falls
es zu jedem
, falls
es zu jedem
![]() ein
ein
![]() gibt,
so daß für alle
gibt,
so daß für alle
![]() und für alle
und für alle ![]() aus
aus
![]() stets
stets
Bemerkung Man vergleiche dies mit der punktweisen Konvergenz:
Für ein Intervall
![]() konvergiere die
Funktionenfolge
konvergiere die
Funktionenfolge ![]() in
in
![]() gleichmäßig auf
gleichmäßig auf ![]() gegen
gegen
![]() .
Sind alle
.
Sind alle ![]() in einem Punkt
in einem Punkt ![]() stetig,
so gilt dies auch für die Grenzfunktion
stetig,
so gilt dies auch für die Grenzfunktion ![]() .
.
Bemerkung. Der Satz gilt entsprechend auch für die rechts-
bzw. linksseitige Stetigkeit in ![]() .
.
Beweis (Stetigkeit der Grenzfunktion).
Es sei
![]() . Da die Folge
. Da die Folge ![]() gleichmäßig gegen
die Grenzfunktion
gleichmäßig gegen
die Grenzfunktion ![]() konvergiert, gibt es ein
konvergiert, gibt es ein
![]() ,
so daß für alle
,
so daß für alle
![]() und für alle
und für alle ![]()
Es sei ![]() eine Menge. Die Norm einer beschränkten
Funktion
eine Menge. Die Norm einer beschränkten
Funktion
![]() wird definiert durch
wird definiert durch
Für ![]() ,
,
![]() und
und
![]() gilt:
gilt:
Beweis .
Eine Funktionenfolge ![]() in
in
![]() konvergiert genau dann gleichmäßig auf
konvergiert genau dann gleichmäßig auf ![]() , wenn gilt:
, wenn gilt:
Beweis .