Es sei ![]() ein kompaktes Intervall.
Eine Funktion
ein kompaktes Intervall.
Eine Funktion
![]() heißt eine
Treppenfunktion, wenn es
endlich viele Punkte
heißt eine
Treppenfunktion, wenn es
endlich viele Punkte
![]() so gibt,
daß für
so gibt,
daß für
![]() die Einschränkung
die Einschränkung
![]() konstant ist.
konstant ist.
Wir stellen für die Integrationstheorie eine Klasse von reellen Funktionen bereit, die sogenannten Regelfunktionen.
Zu den Regelfunktionen gehören die Treppenfunktionen und die stückweise stetigen Funktionen:
Es sei ![]() ein kompaktes Intervall.
Eine Funktion
ein kompaktes Intervall.
Eine Funktion
![]() heißt eine
Treppenfunktion, wenn es
endlich viele Punkte
heißt eine
Treppenfunktion, wenn es
endlich viele Punkte
![]() so gibt,
daß für
so gibt,
daß für
![]() die Einschränkung
die Einschränkung
![]() konstant ist.
konstant ist.
Bemerkung. Die Treppenfunktion ![]() ist also auf den offenenen Intervallen
ist also auf den offenenen Intervallen
![]() konstant.
Die Werte in den Teilpunkten
konstant.
Die Werte in den Teilpunkten ![]() unterliegen keiner
Beschränkung.
unterliegen keiner
Beschränkung.
Es sei ![]() ein kompaktes Intervall. Eine Funktion
ein kompaktes Intervall. Eine Funktion
![]() heißt stückweise stetig,
wenn es endlich viele Punkte
heißt stückweise stetig,
wenn es endlich viele Punkte
![]() so gibt, daß für
so gibt, daß für
![]() die Einschränkung
die Einschränkung
![]() stetig ist und in den Endpunkten einseitige Grenzwerte
in
stetig ist und in den Endpunkten einseitige Grenzwerte
in
![]() :
:
Bemerkung. Die stückweise stetige Funktion ![]() ist also auf den offenenen Intervallen
ist also auf den offenenen Intervallen
![]() stetig und hat eine stetige
Fortsetzung auf die abgeschlossenen Intervalle
stetig und hat eine stetige
Fortsetzung auf die abgeschlossenen Intervalle
![]() .
.
Es gibt keine Vorschrift für die Werte in den Teilpunkten ![]() .
.
Eine stückweise stetige Funktion ist beschränkt.
Es sei
![]() ein Intervall mit
Anfangpunkt
ein Intervall mit
Anfangpunkt
![]() und
Endpunkt
und
Endpunkt
![]() .
Eine Funktione
.
Eine Funktione
![]() heißt eine
Regelfunktion, wenn folgendes gilt:
heißt eine
Regelfunktion, wenn folgendes gilt:
Die Menge der Regelfunktionen auf ![]() wird mit
wird mit
![]() bezeichnet.
bezeichnet.
Bemerkung
Die Definition der Regelfunktion macht keine Vorschrift über die
Lage von ![]() zu den einseitigen Grenzwerten
zu den einseitigen Grenzwerten
![]() und
und ![]() im selben Punkt.
im selben Punkt.
Beispiele von Regelfunktionen sind:
![[*]](crossref.png) ),
),
![[*]](crossref.png) ),
),
![[*]](crossref.png) (3.)) ,
(3.)) ,
Die Rechenregeln ![[*]](crossref.png) für stetige Funktionen gelten sinngemäß für Regelfunktionen.
für stetige Funktionen gelten sinngemäß für Regelfunktionen.
![[*]](crossref.png) )
)
Dagegen ist die Wackelfunktion
(vgl. Beispiel ![[*]](crossref.png) (
(![[*]](crossref.png) .))
keine Regelfunktion, da für die Wackelfunktion in
.))
keine Regelfunktion, da für die Wackelfunktion in ![]() die einseitigen
Grenzwerte nicht existieren.
die einseitigen
Grenzwerte nicht existieren.
Es seien
![]() ein Intervall und
ein Intervall und ![]() eine
Folge von Regelfunktionen auf
eine
Folge von Regelfunktionen auf ![]() , die gleichmäßig auf
, die gleichmäßig auf ![]() gegen eine Funktion
gegen eine Funktion
![]() konvergiert.
konvergiert.
Dann ist die Grenzfunktion ![]() eine Regelfunktion.
eine Regelfunktion.
Beweis . Die Feststellung folgt unmittelbar aus Satz ![[*]](crossref.png)
Es sei ![]() ein kompaktes Intervall.
Für eine Funktion
ein kompaktes Intervall.
Für eine Funktion
![]() sind die folgenden
Aussagen äquivalent:
sind die folgenden
Aussagen äquivalent:
Übungsaufgabe. Man beweise die Ausage des des Korollars
unabhängig, indem man die Beweismethode des Lemmas
![[*]](crossref.png) anpaßt. Man vgl. dazu auch den
Beweis von Satz
anpaßt. Man vgl. dazu auch den
Beweis von Satz ![[*]](crossref.png) .
.
Beweis . ![]() Klar nach Feststellung
Klar nach Feststellung
![[*]](crossref.png)
![]() Zu
Zu
![]() bilde man die Menge
bilde man die Menge
Es ist ![]() .
Sei also
.
Sei also ![]() .
Da
.
Da ![]() Regelfunktion und
Regelfunktion und
![]() ist,
gibt es
ist,
gibt es ![]() mit
mit
![]() , so daß
, so daß
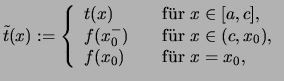
Da ![]() Regelfuntion ist, gibt es
Regelfuntion ist, gibt es
![]() mit
mit
![]() so, daß
so, daß
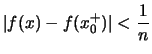 für
für
![$\displaystyle \tilde{t}(x) :=\left\{\begin{array}{ll}
t(x) &\quad\text{f\uml ur...
...\\
f(x_0^+) &\quad\text{f\uml ur \( x\in (x_0,d\,] \).}
\end{array} \right.
$](img2112.png)
Die Folge ![]() konvergiert gleichmäßig auf
konvergiert gleichmäßig auf ![]() gegen
gegen ![]() .
.
![[*]](crossref.png) )
Die Beweismethode des Approximationssatzes wird haüfiger
verwendet. Man spricht von einem Zusammenhangs-Schluß:
)
Die Beweismethode des Approximationssatzes wird haüfiger
verwendet. Man spricht von einem Zusammenhangs-Schluß:
Es sei ![]() ein kompaktes Intervall und
ein kompaktes Intervall und ![]() eine Eigenschaft, die ein Teilintervall
eine Eigenschaft, die ein Teilintervall
![]() haben kann.
Es gelte:
haben kann.
Es gelte:
Aus ![]() und
und ![]() haben
haben ![]() ,
folgt
,
folgt ![]() hat
hat ![]() .
.
Man bilde dann
![]() hat Eigenschaft
hat Eigenschaft ![]() .
.![]() und zeige:
und zeige:
Es seien ![]() ein kompaktes Intervall.
und
ein kompaktes Intervall.
und
![]() eine Regelfunktion.
eine Regelfunktion.
Bemerkung
Analog zu ![[*]](crossref.png) (1.) gibt es eine
monoton fallende Folge von Treppenfunktionen, die gleichmäßig gegen
(1.) gibt es eine
monoton fallende Folge von Treppenfunktionen, die gleichmäßig gegen
![]() konvergiert.
konvergiert.
Beweis .
Für die Treppenfunktionen
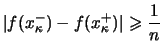
Beweis . Es gibt eine Treppenfunktion
![]() mit
mit
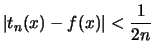 für
für 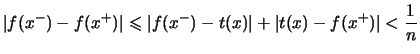 .
.