Bemerkung.
Es seien ![]() ein offenes Intervall,
ein offenes Intervall,
![]() und
und ![]() ein fester Punkt.
ein fester Punkt.
Für eine weiteren Punkt ![]() ,
, ![]() ,
bilde man die Sekante durch die Punkte
,
bilde man die Sekante durch die Punkte
![]() und
und ![]() :
:
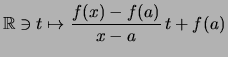 (Sekantengleichung).
(Sekantengleichung).Offensichtlich existiert die Tangente (die Grenzfunktion) genau dann, wenn der Grenzwert der Steigung der Sekanten
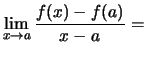 Steigung der Tangente
Steigung der Tangente
Bemerkung. Wir lösen uns von der geometrischen Sprechweise und nennen die Steigung der Sekante Differenzenquotient.
Es seien ![]() ein offenes Intervall,
ein offenes Intervall, ![]() und
und
![]() .
.
Die Funktion
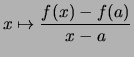 für
für
Sei ![]() ein offenes Intervall.
Eine Funktion
ein offenes Intervall.
Eine Funktion
![]() heißt differenzierbar im Punkt
heißt differenzierbar im Punkt ![]() ,
wenn der Grenzwert
,
wenn der Grenzwert
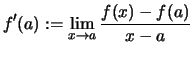
Bemerkung.
Manchmal ist es praktischer, den um ![]() verschobenen
Differenzenquotienten zu betrachten.
verschobenen
Differenzenquotienten zu betrachten.
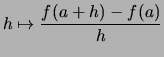 für
für
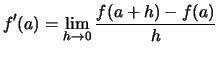 .
.
Es sei ![]() ein offenes Intervall.
Eine Funktion
ein offenes Intervall.
Eine Funktion
![]() heißt
differenzierbar auf
heißt
differenzierbar auf ![]() oder
differenzierbar im Intervall
oder
differenzierbar im Intervall ![]() , wenn
, wenn ![]() in jedem
Punkt des Intervalls
in jedem
Punkt des Intervalls ![]() differenzierbar ist.
differenzierbar ist.
Dann ist die Ableitung ![]() eine Funktion auf
eine Funktion auf ![]() :
:
![]() heißt die abgeleitete Funktion zu
heißt die abgeleitete Funktion zu ![]() oder kurz die Ableitung von
oder kurz die Ableitung von ![]() .
.
Man findet in Literatur weitere Bezeichnungen für die Ableitung,
insbesondere, wenn ![]() für alle
für alle ![]() existiert.
existiert.
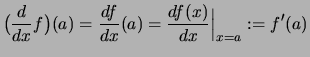 .
.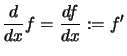 .
.
Bemerkung.
Dann klärt sich auch der oben angedeutete Gebrauch der Differentiale in der Physik.
Bezeichnung.
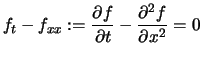 (Wärmeleitungsgleichung).
(Wärmeleitungsgleichung).
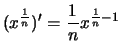 für
für
Beweis .
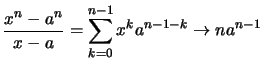 für
für 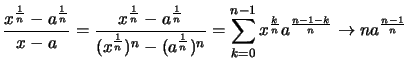 .
.
Ist
![]() an der Stelle
an der Stelle ![]() differenzierbar, dann
ist
differenzierbar, dann
ist ![]() an der Stelle
an der Stelle ![]() stetig.
stetig.
Bemerkung. 1. Die Umkehrung ist falsch, wie das Beispiel der Betragsfunktion zeigt:
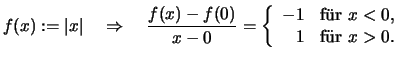
Das erste Beispiel einer solchen Funktion wurde von K. WEIERSTRASS 1861 veröffentlicht. Einige Jahrzehnte zuvor hatte bereits B. BOLZANO ein derartiges Beispiel konstruiert.
3. Für ein einfaches Beispiel von T. TAKAGI (1903) einer nirgends differenzierbaren, stetigen Funktion vergleiche man Kaballo Beispiel 19.15 oder Koenigsberger Kapitel 9.11.
Beweis (differenzierbar
![]() stetig).
stetig).
Man schreibe ![]() in der Form:
in der Form:
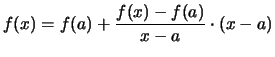 für
für
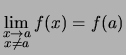 .
.