Es sei ![]() ein offenes Intervall.
Die Funktionen
ein offenes Intervall.
Die Funktionen
![]() seien im Punkt
seien im Punkt ![]() differenzierbar.
differenzierbar.
Dann sind auch die Funktionen
Es gelten die Rechenregeln:
- Linearität:
-
![$\textstyle \parbox{50em}{
\( (f+g)'(a) = f'(a)+g'(a) \),
\\ [.5ex]
\( (\lambda\,f)'(a) = \lambda\,f'(a) \)f\uml {u}r \( \lambda\in\mathbb{R}\) .\strut }$](img2664.png)
- Produktregel:
-
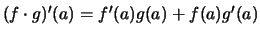 .
.
- Quotientenregel:
-
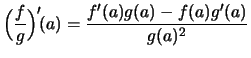 .
.
Es sei ![]() ein offenes Intervall.
Die Funktionen
ein offenes Intervall.
Die Funktionen
![]() seien im Punkt
seien im Punkt ![]() differenzierbar.
differenzierbar.
Dann sind auch die Funktionen
Es gelten die Rechenregeln:
![$\textstyle \parbox{50em}{
\( (f+g)'(a) = f'(a)+g'(a) \),
\\ [.5ex]
\( (\lambda\,f)'(a) = \lambda\,f'(a) \)f\uml {u}r \( \lambda\in\mathbb{R}\) .\strut }$](img2664.png)
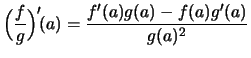 .
.
Bemerkung. 1. Man präge sich die Produktregel in dieser Reihenfolge ein:
Beispiel: Funktionen mit Werten in den Matrizen und das Matrizenprodukt oder für das Skalarprodukt vektorwertiger Funktionen.
2. Wir führen auch den Beweis der Quotientenregel so, daß er sich leicht auf die Inversenbildung in anderen Produkten übertragen läßt.
Beweis (Rechenregeln der Ableitung).
Linearität:
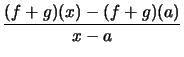
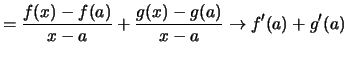 für
für 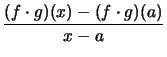
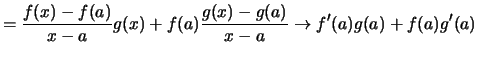 .
.
Da
![]() ist, existiert
ist, existiert ![]() in einer
Umgebung von
in einer
Umgebung von ![]() .
.
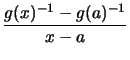 |
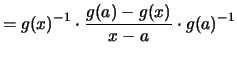 |
|
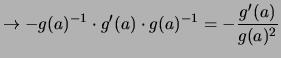 . . |
Bemerkung.
Mit den Rechenregeln ![[*]](crossref.png) kann man Polynome und
rationale Funktionen
differenzieren.
kann man Polynome und
rationale Funktionen
differenzieren.
Beweis .
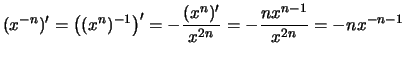 .
.