




Next: The mappings
Up: Basic facts
Previous: Basic facts
Contents
Index
Let  be a complex vector space. A matrix seminorm [EW97b] is
a family of mappings
be a complex vector space. A matrix seminorm [EW97b] is
a family of mappings
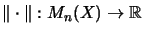 , one on each matrix level1
, one on each matrix level1
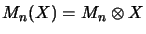 for
for
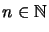 , such that
, such that
(R1)
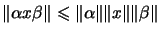
for all
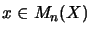
,
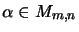
,
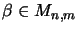
(R2)
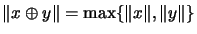
for all
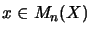
,
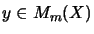
.
2
Then every one of these mappings
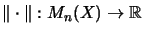 is a seminorm. If one (and
then every one) of them is definite, the operator space seminorm is called a
matrix norm.
is a seminorm. If one (and
then every one) of them is definite, the operator space seminorm is called a
matrix norm.
A
matricially normed space
is a complex vector space with a matrix norm. It can be defined equivalently, and is
usually defined in the literature,
as a complex vector space with a family of norms with (R1) and (R2) on its matrix
levels.
If 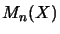 with this norm is complete for one
with this norm is complete for one 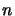 (and then for all
(and then for all 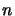 ), then
), then
 is called an
operator space3([Rua88], cf. [Wit84a]).
is called an
operator space3([Rua88], cf. [Wit84a]).
For a matricially normed space (operator space)  the spaces
the spaces 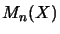 are normed spaces (Banach spaces).4These are called the matrix levels of
are normed spaces (Banach spaces).4These are called the matrix levels of  (first matrix level,
second level...).
(first matrix level,
second level...).
The operator space norms on a fixed vector space  are partially ordered by the
pointwise order on each matrix level
are partially ordered by the
pointwise order on each matrix level 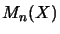 . One says that a greater operator space
norm dominates a smaller one.
. One says that a greater operator space
norm dominates a smaller one.
Footnotes
- ... level1
-
The term matrix level is to be found for instance in
- ....2
-
It suffices to show one of the following two weaker conditions:
(R1
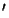
)
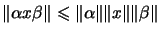
for all
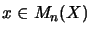
,
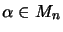
,
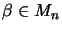
,
(R2)
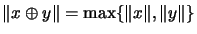
for all
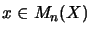
,
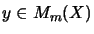
,
(R1)
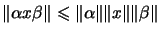
for all
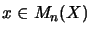
,
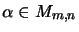
,
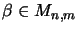
,
(R2
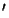
)
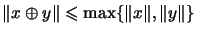
for all
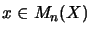
,
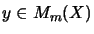
,
- ... space3
-
In the literature, the terminology is not conseqent. We propose this distinction
between matricially normed space and operator space
in analogy with normed space and
Banach space.
- ... spaces).4
-
In the literature, the normed space
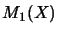 usually is denoted also by
usually is denoted also by  .
We found that a more distinctive notation is sometimes usefull.
.
We found that a more distinctive notation is sometimes usefull.





Next: The mappings
Up: Basic facts
Previous: Basic facts
Contents
Index
Prof. Gerd Wittstock
2001-01-07
![]() is a seminorm. If one (and
then every one) of them is definite, the operator space seminorm is called a
matrix norm.
is a seminorm. If one (and
then every one) of them is definite, the operator space seminorm is called a
matrix norm.
![]() with this norm is complete for one
with this norm is complete for one ![]() (and then for all
(and then for all ![]() ), then
), then
![]() is called an
operator space3([Rua88], cf. [Wit84a]).
is called an
operator space3([Rua88], cf. [Wit84a]).
![]() the spaces
the spaces ![]() are normed spaces (Banach spaces).4These are called the matrix levels of
are normed spaces (Banach spaces).4These are called the matrix levels of ![]() (first matrix level,
second level...).
(first matrix level,
second level...).
![]() are partially ordered by the
pointwise order on each matrix level
are partially ordered by the
pointwise order on each matrix level ![]() . One says that a greater operator space
norm dominates a smaller one.
. One says that a greater operator space
norm dominates a smaller one.