




Next: Complete boundedness
Up: Completely bounded bilinear mappings
Previous: Amplification
Contents
Index
Jointly
complete boundedness
Let 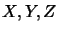 be operator spaces.
A bilinear mapping
be operator spaces.
A bilinear mapping
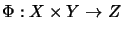 is called
jointly completely bounded
[BP91, Def. 5.3 (jointly completely bounded)]
if the norms of the
joint amplifications
of
is called
jointly completely bounded
[BP91, Def. 5.3 (jointly completely bounded)]
if the norms of the
joint amplifications
of 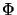 are uniformly bounded:
where
are uniformly bounded:
where
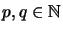 ,
,
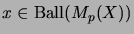 ,
,
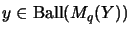 [BP91, Def. 5.3].
The norm
[BP91, Def. 5.3].
The norm
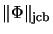 equals the norm
equals the norm
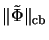 of the linearization
on the projective operator space tensor product.
of the linearization
on the projective operator space tensor product.
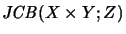 denotes the operator space consisting of the jointly completely bounded
bilinear maps.
One obtains a norm on each matrix level by the identification
We have
completely isometrically.
By taking the transposition
denotes the operator space consisting of the jointly completely bounded
bilinear maps.
One obtains a norm on each matrix level by the identification
We have
completely isometrically.
By taking the transposition
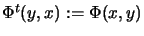 we obtain a
complete isometry
we obtain a
complete isometry
Prof. Gerd Wittstock
2001-01-07