Bemerkung. Wir formulieren die Definition der Ableitung so um, daß man nicht mehr den Grenzwert eines Quotienten untersucht. Dies bringt folgende Vorteile:
Die Sätze und Beweise mit der äquivalenten Definition gelten sinngemäß auch für Funktionen von Vektoren.
Bemerkung.
Es sei ![]() differenzierbar im Punkte
differenzierbar im Punkte ![]() .
.
Wir bezeichnen den verschobenen Differenzenquotienten und
seinen Grenzwert bei ![]() für
für
![]() mit
mit
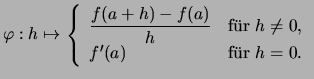
Es seien
![]() ein offenes Intervall,
ein offenes Intervall, ![]() . und
. und
![]() .
Die folgenden Aussagen sind äquivalent:
.
Die folgenden Aussagen sind äquivalent:
Beweis . ![]() Vergleiche die Vorbemerkung.
Vergleiche die Vorbemerkung.
![]() Nach Voraussetzung existiert
Nach Voraussetzung existiert
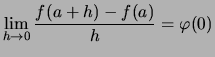
Seien
![]() offene Intervalle und
offene Intervalle und
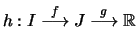
Bemerkung. Die Ableitung der Komposition ![]() ist das Produkt der Ableitungen
der äußeren Funktion
ist das Produkt der Ableitungen
der äußeren Funktion ![]() mit der Ableitung der inneren
Funktion
mit der Ableitung der inneren
Funktion ![]() :
:

Bemerkung. Die Kettenregel gilt auch für Abbildungen zwischen Vektorräumen. Deren Ableitungen sind Matrizen und das Matrizenprodukt ist nicht kommutativ.
Man präge sich deshalb die Kettenregel in dieser Reihenfolge ein:
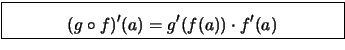
Beweis . Nach Lemma ![[*]](crossref.png) gibt es
eine stetige Funktion
gibt es
eine stetige Funktion
Setzt man
![]() so folgt
so folgt
![[*]](crossref.png)
Bemerkung. Wenn
![]() ein offenes Intervall
und
ein offenes Intervall
und
![]() stetig und streng monoton ist, dann
ist
stetig und streng monoton ist, dann
ist ![]() ein offenes Intervall
(vgl.
ein offenes Intervall
(vgl. ![[*]](crossref.png) ).
).
Wenn ![]() und die Umkehrfunktion
und die Umkehrfunktion ![]() differenzierbar sind,
so folgt aus derKettenregel
differenzierbar sind,
so folgt aus derKettenregel
![]() und somit
und somit
Es seien
![]() ein offenes Intervall,
ein offenes Intervall,
![]() stetig, streng monoton,
stetig, streng monoton, ![]() und
und
![]() die Umkehrfunktion zu
die Umkehrfunktion zu ![]() .
Es sei
.
Es sei ![]() im Punkt
im Punkt ![]() differenzierbar.
differenzierbar.
Die Umkehrfunktion ![]() ist genau dann an der Stelle
ist genau dann an der Stelle ![]() differenzierbar, wenn
differenzierbar, wenn
![]() .
In diesem Fall gilt
.
In diesem Fall gilt
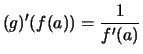 .
.
Beweis (Ableitung der Umkehrfunktion).
![]() Man vergleiche die Vorbemerkung.
Man vergleiche die Vorbemerkung.
![]() Nach Lemma
Nach Lemma ![[*]](crossref.png) gibt es
eine stetige Funktion
gibt es
eine stetige Funktion
![]() mit:
mit:
Man definiere eine stetige Funktion
![]() durch:
durch:
 mit mit |
![[*]](crossref.png) folgt
die Differenzierbarkeit von
folgt
die Differenzierbarkeit von