Unser Arbeitsgebiet: Algebraische Geometrie und Computeralgebra

Klassische Algebraische Geometrie ist die Theorie von algebraischen Kurven, Flächen, 3-Mannigfaltigkeiten, etc., sowie deren Modulräumen. Aktuelle Forschungsergebnisse werden unter anderem auf regelmäßig stattfindenden Oberwolfach-Workshops präsentiert: 2012,  2010,  2008,  2006,  2004,  2002,  2000,  1998,  1995.

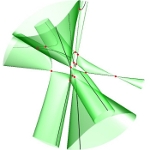
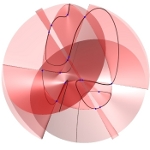
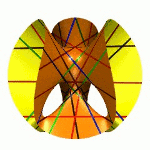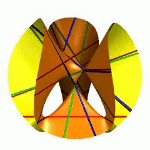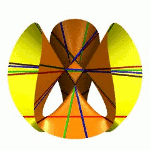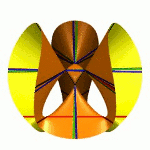
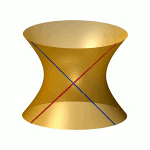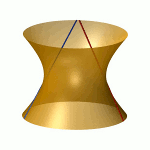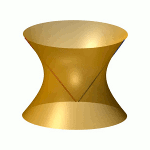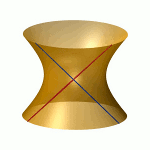
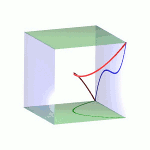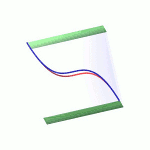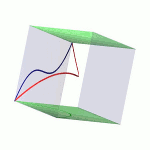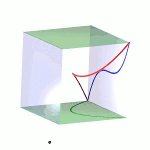
Ihr Ursprung liegt in dem Studium der Lösungen algebraischer Gleichungssysteme. Es ist ein Spezifikum der algebraischen Geometrie, dass deren Objekte in Familien auftreten, denn man kann die Koeffizienten des Gleichungssystems variieren. Das systematische Studium der Parameterräume für die Koeffizienten führt zu dem Konzept der Modulräume.Das Bild zeigt die drei Mitglieder der Familie x2+y2-z2+a mit den Werten a=-1, 0, +1.

Moderne Computeralgebra erlaubt es, Gleichungssysteme numerisch und symbolisch zu studieren und führt die algebraische Geometrie damit zu ihren Wurzeln zurück.

In unserer Arbeitsgruppe wird die algebraische Geometrie in ihrer ganzen Breite betrieben, von der Theorie über Konstruktionen bis zur Computeralgebra. Anwendungen erstrecken sich von der theoretischen Physik (insbesondere der Stringtheorie) über algebraische Statistik und Visualisierung bis hin zum Mechanical Engeneering.