Let ![]() be an operator system. We define norms by
be an operator system. We define norms by
If ![]() is any unital completely positve embedding from
is any unital completely positve embedding from ![]() into some
into some ![]() (cf. section
(cf. section ![[*]](crossref.png) ) then
) then
![]() for all
for all
![]() and
and
![]() . This holds because
. This holds because
![]() if and only if
if and only if
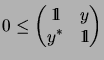
Let ![]() and
and ![]() be operator systems and let
be operator systems and let
![]() be completely positive. We supply
be completely positive. We supply ![]() and
and ![]() with the norms from equation
(
with the norms from equation
(![[*]](crossref.png) ). Then
). Then ![]() is completely bounded and
is completely bounded and
![]() (cf. [Pau86, Proposition 3.5]).
(cf. [Pau86, Proposition 3.5]).