




Next: Multiplicative Structures
Up: Hilbertian Operator Spaces
Previous: Characterizations
Contents
Index
Let  ,
, 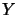 be operator spaces. We say that a linear map
be operator spaces. We say that a linear map
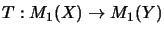 factors through a
column Hilbert space ,
if there is a Hilbert space
factors through a
column Hilbert space ,
if there is a Hilbert space 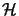 and completely bounded maps
and completely bounded maps
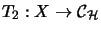 ,
,
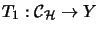 with
with
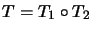 .
We define
.
We define
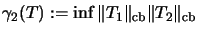
,
where the infimum runs over all possible factorizations.
If no such factorisation exists we say
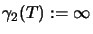 .
.
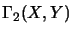 is the Banach space of all linear
maps
is the Banach space of all linear
maps
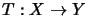 with
with
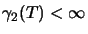 [ER91, Chap. 5],[Ble92b, p. 83].
[ER91, Chap. 5],[Ble92b, p. 83].
Let 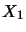 and
and 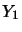 be operator spaces
and
be operator spaces
and
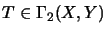 ,
,
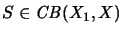 ,
,
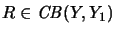 .
Then we have the
.
Then we have the
 ideal property
ideal property
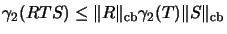
.
We interpret a matrix
![$ T=[T_{ij}] \in M_n(\Gamma_2(X,Y))$](img441.png) as a mapping
from
as a mapping
from  to
to
 :
:
:=[T_{ij}(x)]$](img443.png) .
.
 has a factorization in completely bounded mappings
has a factorization in completely bounded mappings
Again, we define
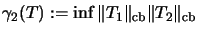
,

where the infimum is taken over all factorizations.
So we get an operator space structure on
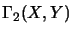 [ER91, Cor. 5.4].
[ER91, Cor. 5.4].
Let 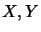 be operator spaces and
be operator spaces and 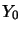 an
operator subspace of
an
operator subspace of 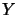 .
Then the inclusion
.
Then the inclusion
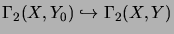 is completely isometric [ER91, Prop. 5.2].
is completely isometric [ER91, Prop. 5.2].
Let  ,
, 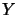 be operator spaces. It is well known that
every linear map
be operator spaces. It is well known that
every linear map
defines a linear functional
via
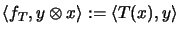
.
This identification determines the complete isometry
[ER91, Thm. 5.3] [Ble92b, Thm. 2.11]
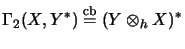
.
Let  ,
, 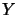 ,
, 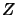 be operator spaces.
We get a complete isometry
via the mapping
be operator spaces.
We get a complete isometry
via the mapping
[ER91, Cor. 5.5].





Next: Multiplicative Structures
Up: Hilbertian Operator Spaces
Previous: Characterizations
Contents
Index
Prof. Gerd Wittstock
2001-01-07
![]() and
and ![]() be operator spaces
and
be operator spaces
and
![]() ,
,
![]() ,
,
![]() .
Then we have the
.
Then we have the
![]() ideal property
ideal property
![]() as a mapping
from
as a mapping
from ![]() to
to
![]() :
:
![]() .
.
![]() has a factorization in completely bounded mappings
has a factorization in completely bounded mappings
![]() be operator spaces and
be operator spaces and ![]() an
operator subspace of
an
operator subspace of ![]() .
Then the inclusion
.
Then the inclusion
![]() is completely isometric [ER91, Prop. 5.2].
is completely isometric [ER91, Prop. 5.2].
![]() ,
, ![]() be operator spaces. It is well known that
every linear map
be operator spaces. It is well known that
every linear map