With the following
operator space structures , ![]() is completely isometrically
isomorphic to an operator algebra:
is completely isometrically
isomorphic to an operator algebra:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
More generally: The space ![]() is completely isometrically isomorphic to an operator algebra, if endowed with an operator space
structure which
dominate
dominates both
is completely isometrically isomorphic to an operator algebra, if endowed with an operator space
structure which
dominate
dominates both
![]() and
and
![]() .
.
With the following operator space structures, ![]() is not completely isomorphic to an operator algebra:
is not completely isomorphic to an operator algebra:
![]() ,
,
![]() .
.
More generally: The space ![]() is not completely isomorphic to an operator algebra,
if endowed with an operator space structure which is
dominate
dominated by both
is not completely isomorphic to an operator algebra,
if endowed with an operator space structure which is
dominate
dominated by both
![]() and
and
![]() .
.
In the extreme cases ![]() resp.
resp. ![]() , we have two opposite results [BLM95, Thm. 3.1]:
, we have two opposite results [BLM95, Thm. 3.1]:
- Equipped with any operator space structure,
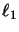 is completely isometrically
isomorphic to an operator algebra.
is completely isometrically
isomorphic to an operator algebra.
-
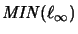 is, up to complete isomorphy, the only operator algebra structure on
is, up to complete isomorphy, the only operator algebra structure on
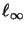 .
.
For
![]() the following holds true (cf. [BLM95, Thm. 3.4]):
the following holds true (cf. [BLM95, Thm. 3.4]):
-
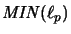 is completely isomorphic to an operator algebra if and only if
is completely isomorphic to an operator algebra if and only if 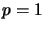 or
or 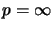 .
.
-
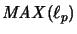 , in case
, in case
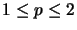 , is completely isometrically
isomorphic to an operator algebra.
In all the other cases
, is completely isometrically
isomorphic to an operator algebra.
In all the other cases
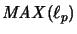 is not completely isomorphic to an operator algebra.
is not completely isomorphic to an operator algebra.
On the contrary, the operator space structure on the ![]() spaces obtained
via complex
interpolation
always defines an operator algebra structure.
More precisely [BLM95, Cor. 3.3]:
spaces obtained
via complex
interpolation
always defines an operator algebra structure.
More precisely [BLM95, Cor. 3.3]:
For each
![]() ,
, ![]() is completely isometrically
isomorphic to an operator algebra.
is completely isometrically
isomorphic to an operator algebra.
We write ![]() for the operator space structure defined on
for the operator space structure defined on ![]() by G. Pisier. This operator space structure is obtained by
complex interpolation between
by G. Pisier. This operator space structure is obtained by
complex interpolation between
![]() and
and
![]() .
.
- (a)
- Let us first consider the usual product on the Schatten classes
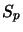 .
Here we have the following negative result [BLM95, Thm. 6.3]:
For each
.
Here we have the following negative result [BLM95, Thm. 6.3]:
For each
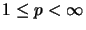 , the operator space
, the operator space 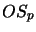 with the usual product is not completely isomorphic
to an operator algebra.
with the usual product is not completely isomorphic
to an operator algebra.
- (b)
- Consider now the Schur product on the Schatten classes
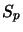 .
Here we obtain positive results, even for different operator space structures:
.
Here we obtain positive results, even for different operator space structures:
Caution is advised: The space ![]() (and likewise
(and likewise
![]() ), whether endowed with the usual or the Schur product,
is not completely isomorphic to an operator algebra [BLM95, Thm. 6.3].
), whether endowed with the usual or the Schur product,
is not completely isomorphic to an operator algebra [BLM95, Thm. 6.3].