



Next: Module tensor products
Up: Completely bounded bilinear mappings
Previous: Complete boundedness
Contents
Index
Representation
Completely
bounded bilinear forms were first studied on C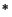 -algebras
-algebras
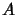 ,
, 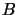 [EK87].
For a bilinear form
[EK87].
For a bilinear form
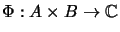 the following properties are equivalent:
the following properties are equivalent:
- (1)
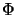 is completely bounded.
is completely bounded.
- (2)
- There is a constant
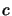 such that
for all
such that
for all
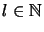 ,
, 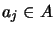 ,
, 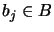 .
.
- (3)
- There is a constant
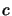 and states
and states
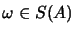 ,
,
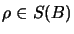 such that
for all
such that
for all 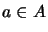 ,
, 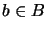 .
.
- (4)
- There exist
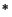 -representations
-representations
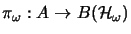 and
and
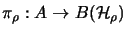 with cyclic vectors
with cyclic vectors
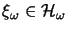 ,
,
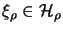 and an operator
and an operator
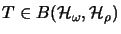 such that
such that
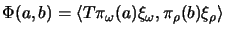 for all
for all 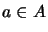 ,
, 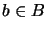 .
.
One can choose
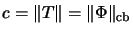 and
and
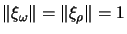 .52
.52
Footnotes
- ....52
- For further references see
[CS89, Sec. 4].
Prof. Gerd Wittstock
2001-01-07