



Next: Interpolation
Up: Tensor products
Previous: Joint amplification of a
Contents
Index
The definition of the
completely bounded
bilinear maps as well as the
Haagerup tensor product
relies on the
tensor
matrix multiplication
[Eff87]
of operator matrices
![$ x = [x_{ij}] \in M_{n,l}(X)$](img891.png) ,
,
![$ y = [y_{jk}]\in M_{l,n}(Y)$](img892.png) .
.
The
amplification
of the bilinear mapping
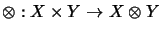 is given by
is given by
For scalar matrices
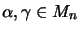 ,
,
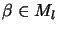 we have
we have
We use the short hand notation
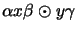 .
.
For linear maps
we denote by
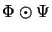 the mapping
We then have
for
the mapping
We then have
for
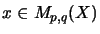 ,
,
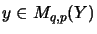 .
Let
.
Let
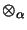 be an
operator space tensor product .
We define the
tensor matrix multiplication
be an
operator space tensor product .
We define the
tensor matrix multiplication
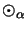 of operator matrices
of operator matrices
![$ S = [S_{i,j}] \in M_{n,l}(\mathit{CB}(X_1,X_2))$](img1359.png) ,
,
![$ T = [T_{k,l}] \in M_{l,n}(\mathit{CB}(Y_1,Y_2))$](img1360.png) of completely bounded maps by setting
of completely bounded maps by setting




Next: Interpolation
Up: Tensor products
Previous: Joint amplification of a
Contents
Index
Prof. Gerd Wittstock
2001-01-07
![]() is given by
is given by
![]() ,
,
![]() we have
we have
![$\displaystyle \Phi \odot \Psi =
\left[\sum_{j=1}^l \Phi_{ij} \otimes \Psi_{jk}\right] :
X \otimes Y \rightarrow M_{n}(V \otimes W),
$](img1353.png)
![$\displaystyle \Phi \odot \Psi : x \otimes y \mapsto
\left[\sum_{j=1}^l \Phi_{ij}(x) \otimes \Psi_{jk}(y) \right].
$](img1354.png)
![$\displaystyle S \odot_\alpha T = \left[\sum_{j=1}^l S_{ij} \otimes_\alpha T_{jk}\right]
\in M_n(\mathit{CB}(X_1 \otimes_\alpha Y_1, X_2 \otimes_\alpha Y_2)).
$](img1361.png)