




Next: Jointly complete boundedness
Up: Completely bounded bilinear mappings
Previous: Completely bounded bilinear mappings
Contents
Index
In the literature, there are two different notions of an
amplification
of a bilinear mapping.
We shall call the first kind
![[*]](crossref.png) of amplification the
joint
amplification.
This joint amplification is needed to obtain a matrix duality
- which is
fundamental in the duality theory of operator spaces -,
starting from an ordinary duality
of amplification the
joint
amplification.
This joint amplification is needed to obtain a matrix duality
- which is
fundamental in the duality theory of operator spaces -,
starting from an ordinary duality
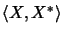 .
The notion of joint amplification leads to the
jointly completely bounded
bilinear maps as well as the
projective operator space tensor product.
We will speak of the second kind
.
The notion of joint amplification leads to the
jointly completely bounded
bilinear maps as well as the
projective operator space tensor product.
We will speak of the second kind
![[*]](crossref.png) of an amplification as the
amplification
of a bilinear mapping.
This notion leads to the
completely bounded
bilinear maps and the
Haagerup tensor product.
In the sequel, we will use the notation
of an amplification as the
amplification
of a bilinear mapping.
This notion leads to the
completely bounded
bilinear maps and the
Haagerup tensor product.
In the sequel, we will use the notation
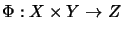 for a bilinear mapping and
for a bilinear mapping and
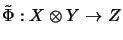 for its linearization.
Both notions of an amplification of a bilinear map
for its linearization.
Both notions of an amplification of a bilinear map
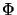 are formulated in terms of the
amplification of its linearization:
are formulated in terms of the
amplification of its linearization:
-
The
joint amplification of
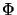 produces
the bilinear mapping
of the operator matrices
produces
the bilinear mapping
of the operator matrices
![$ x = [x_{ij}] \in M_{p}(X)$](img887.png) and
and
![$ y = [y_{kl}] \in M_{q}(Y)$](img888.png) .
Here,
the tensor product of operator matrices is
defined
via
.
Here,
the tensor product of operator matrices is
defined
via
-
In
the case of
completely bounded
bilinear maps one deals with the
tensor
matrix multiplication
[Eff87]
of operator matrices
![$ x = [x_{ij}] \in M_{n,l}(X)$](img891.png) and
and
![$ y = [y_{jk}]\in M_{l,n}(Y)$](img892.png) .
For more formulae, see:
tensor matrix multiplication .
The (n,l)-th
amplification
of a bilinear map
.
For more formulae, see:
tensor matrix multiplication .
The (n,l)-th
amplification
of a bilinear map
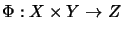 is defined by
is defined by
for
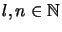 ,
,
![$ x = [x_{ij}] \in M_{n,l}(X)$](img891.png) ,
,
![$ y = [y_{jk}]\in M_{l,n}(Y)$](img892.png) .
In case
.
In case 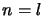 , we shortly write48
, we shortly write48
Footnotes
- ... write48
- In the literature, the amplification of a bilinear map often is defined only for
quadratic operator matrices and is called
the amplification
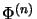 .
Nevertheless,
we will also be dealing with the amplification for rectangular matrices
since this permits
the formulation of
statements
where for fixed
.
Nevertheless,
we will also be dealing with the amplification for rectangular matrices
since this permits
the formulation of
statements
where for fixed
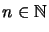 all amplifications
all amplifications
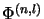 ,
,
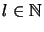 , are considered.
, are considered.





Next: Jointly complete boundedness
Up: Completely bounded bilinear mappings
Previous: Completely bounded bilinear mappings
Contents
Index
Prof. Gerd Wittstock
2001-01-07
![[*]](crossref.png) of amplification the
joint
amplification.
This joint amplification is needed to obtain a matrix duality
- which is
fundamental in the duality theory of operator spaces -,
starting from an ordinary duality
of amplification the
joint
amplification.
This joint amplification is needed to obtain a matrix duality
- which is
fundamental in the duality theory of operator spaces -,
starting from an ordinary duality
![[*]](crossref.png) of an amplification as the
amplification
of a bilinear mapping.
This notion leads to the
completely bounded
bilinear maps and the
Haagerup tensor product.
In the sequel, we will use the notation
of an amplification as the
amplification
of a bilinear mapping.
This notion leads to the
completely bounded
bilinear maps and the
Haagerup tensor product.
In the sequel, we will use the notation