



Next: Interpolation
Up: Interpolation
Previous: Interpolation
Contents
Index
Let 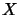 and
and 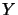 be operator spaces such that
be operator spaces such that 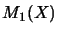 and
and 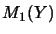 are embedded in
a Hausdorff topological vector space.
are embedded in
a Hausdorff topological vector space.
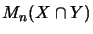 is given a norm via
is given a norm via
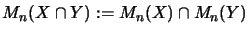 .
So we have:
.
So we have:
![$\displaystyle { \left\Norm [x_{ij}] \right\Norm }_{M_n(X \cap Y)}
= \max \left...
...\right\Norm }_{M_n(X)} , { \left\Norm [x_{ij}] \right\Norm }_{M_n(Y)}
\right\}$](img1365.png)
.

The operator space 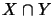 is called the
intersection of
is called the
intersection of 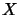 and
and 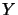 .
.
For operator spaces75 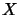 and
and 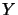 , by embedding
, by embedding
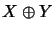 in
in
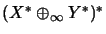 we obtain an operator space structure
we obtain an operator space structure
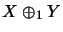 .
We write
.
We write
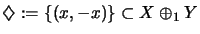 .
The quotient operator space
.
The quotient operator space
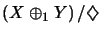 is called the
sum of
is called the
sum of 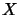 and
and 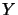 and is denoted by
and is denoted by 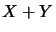 .
We have
.
We have
![$\displaystyle { \left\Norm [x_{ij}] \right\Norm }_{M_n(X+Y)}
= \inf_{[x_{ij}] ...
...{ \left\Norm [\left(x_{ij_X},x_{ij_Y}\right)] \right\Norm }_{M_n(X \oplus_1 Y)}$](img1377.png)
.
Footnotes
- ... spaces75
-
Let
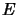 ,
, 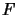 be Banach spaces. Then we have their 1-direct sum
be Banach spaces. Then we have their 1-direct sum
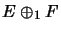 with the norm
and their sum
with the norm
and their sum 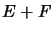 with the quotient norm
with the quotient norm
Prof. Gerd Wittstock
2001-01-07