Man setze
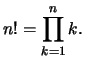
Man setze
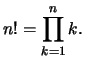
Es ist ![]() die Anzahl der möglichen Anordnungen (Permutationen)
einer Menge aus
die Anzahl der möglichen Anordnungen (Permutationen)
einer Menge aus ![]() Elementen.
Elementen.
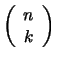 die Anzahl der
möglichen Auswahlen von
die Anzahl der
möglichen Auswahlen von
Anmerkung: Es ist
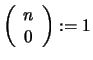 .
.
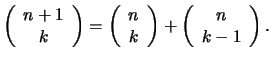
Aus diesem Lemma erhalten wir das Pascalsche Dreieck:
| n=0 | 1 | ||||||||
| n=1 | 1 | 1 | |||||||
| n=2 | 1 | 2 | 1 | ||||||
| n=3 | 1 | 3 | 3 | 1 | |||||
| n=4 | 1 | 4 | 6 | 4 | 1 |
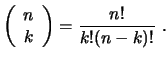
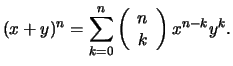
Anmerkung.
Man vergleiche die ähnliche zweite binomische Formel
![[*]](crossref.png) (
(![[*]](crossref.png) )
)