Es sei
![]() eine Abbildung.
eine Abbildung.
- Für
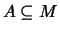 erklären wir durch
das Bild von A. Es ist
erklären wir durch
das Bild von A. Es ist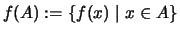
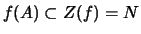 .
.
- Für
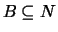 erklären wir durch
das Urbild von B. Es ist
erklären wir durch
das Urbild von B. Es ist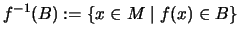
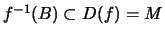 .
.
Es sei
![]() eine Abbildung.
eine Abbildung.
Anmerkung. Man unterscheide
![]() und den Zielbereich
und den Zielbereich ![]() einer Abbildung.
einer Abbildung.
Eine Abbildung
![]() heißt
heißt
Anmerkung: Für eine Abbildung
![]() gilt:
gilt:
Es sei
![]() .
Die folgenden Aussagen sind äquivalent:
.
Die folgenden Aussagen sind äquivalent:
Es sei
![]() eine bijektive Abbildung.
Die Umkehrabbildung
eine bijektive Abbildung.
Die Umkehrabbildung