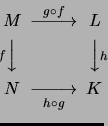Nächste Seite: Endliche Mengen
Aufwärts: Abbildungen
Vorherige Seite: Umkehrabbildung
Inhalt
Wenn der Zielbereich einer Abbildung 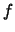 im Definitionsbereich einer
weiteren Abbildung
im Definitionsbereich einer
weiteren Abbildung 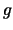 enthalten ist, können wir die beiden
Abbildungen nacheinander ausführen:
enthalten ist, können wir die beiden
Abbildungen nacheinander ausführen:
Definition 1.3.15 (Komposition)
Für Abbildungen
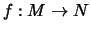 ,
,
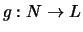 definiert man die
Komposition
definiert man die
Komposition
durch
für alle
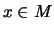
.
Anmerkung
- Sprich
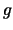 nach
nach 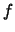 für die zusammengesetzte Abbildung
für die zusammengesetzte Abbildung 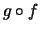 .
.
- Statt Komposition sagt man auch Zusammensetzung, Hintereinanderausführung
oder Verkettung.
- Die Komposition bindet stärker als das Argument:
Um Mißverständnisse zu vermeiden,
sollte man die Klammern aber setzen.
- In längeren Formeln schreibt man statt
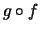 auch
auch
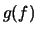
oder
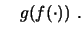
- Man kann die Komposition auch anschaulicher als Diagramm schreiben:
Beispiel.
Auch wenn 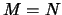 ist, so ist im allgemeinen
ist, so ist im allgemeinen
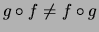 .
Z.B.:
.
Z.B.:
Dann ist
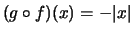 und
und
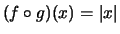 .
.
Feststellung 1.3.16 (Assoziativgesetz der Komposition)
Für
gilt
Man kann also kurz
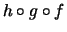
schreiben.
Wir veranschaulichen das Resultat als kommutierendes Diagramm:
Feststellung 1.3.17 (Umkehrabbildung)
Eine Abbildung
ist genau dann
bijektiv, wenn eine
Abbildung
so existiert, daß
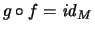
und
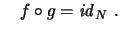
Dann ist
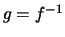
.
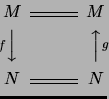
Als kommutatives Diagramm sieht das so aus:




Nächste Seite: Endliche Mengen
Aufwärts: Abbildungen
Vorherige Seite: Umkehrabbildung
Inhalt
Analysis1-A.Lambert
2001-02-09
![]() im Definitionsbereich einer
weiteren Abbildung
im Definitionsbereich einer
weiteren Abbildung ![]() enthalten ist, können wir die beiden
Abbildungen nacheinander ausführen:
enthalten ist, können wir die beiden
Abbildungen nacheinander ausführen:
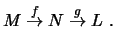
![]() ist, so ist im allgemeinen
ist, so ist im allgemeinen
![]() .
Z.B.:
.
Z.B.:
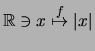
![]() und
und
![]() .
.