



Nächste Seite: Kartesisches Produkt
Aufwärts: Abbildungen
Vorherige Seite: Komposition von Abbildungen
Inhalt
Bemerkung 1.3.18 (Mengen
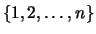
)
- Es seien
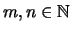 und
und 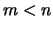 .
.
- a)
- Es gibt keine injektive Abbildung
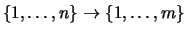 .
.
- b)
- Es gibt keine surjektive Abbildung
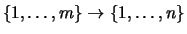 .
.
- Es sei
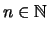 .
Für jede Abbildung
gilt:
.
Für jede Abbildung
gilt:
- Eine bijektive Abbildung
heißt eine Permutationen der Menge
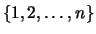 .
.
Bemerkung 1.3.20 (endliche Mengen)
- Eine Menge
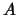 heißt endlich, wenn es ein
heißt endlich, wenn es ein
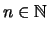 und
eine surjektive Abbildung
gibt oder
und
eine surjektive Abbildung
gibt oder
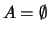 ist.
ist.
Man schreibt dann die Werte in der Form 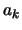 ,
,
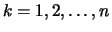 ,
und kürzt den Sachverhalt folgendermaßen ab:
,
und kürzt den Sachverhalt folgendermaßen ab:
- Zu einer endlichen Menge
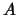 gibt es immer eine natürliche Zahl
gibt es immer eine natürliche Zahl
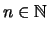 und eine bijektive Abbildung (Aufzählung)
und eine bijektive Abbildung (Aufzählung)
Die Zahl 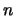 heißt die Anzahl der Elemente von
heißt die Anzahl der Elemente von 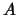 oder die
Mächtigkeit von
oder die
Mächtigkeit von 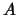 .
.
Auf Grund von
Bemerkung ![[*]](crossref.png) ist die Mächtigkeit einer endlichen Menge wohldefiniert.
ist die Mächtigkeit einer endlichen Menge wohldefiniert.
- Es kommt auf die Reihenfolge der Aufzählung nicht an.
Hat man eine andere Aufzählung, so gibt es eine Permutation
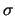 von
von
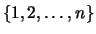 ,
so daß die andere Aufzählung die Form
,
so daß die andere Aufzählung die Form
hat:
- Auf Grund von Bemerkung
![[*]](crossref.png) ist eine Teilmenge
ist eine Teilmenge 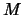 einer endlichen Menge
einer endlichen Menge 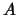 endlich.
endlich.
Wenn die Teilmenge 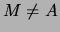 ist, so ist
die Mächtigkeit von
ist, so ist
die Mächtigkeit von 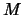 kleiner als die Mächtigkeit von
kleiner als die Mächtigkeit von 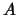 .
.
- Es sei
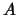 eine endliche Menge und
eine endliche Menge und
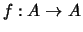 .
Dann gilt:
.
Dann gilt:
Beweis . Zum Begriff der endlichen Menge vgl. Bemerkung ![[*]](crossref.png) .
Wir zeigen die folgende Behauptung durch vollständige Induktion:
.
Wir zeigen die folgende Behauptung durch vollständige Induktion:
Eine Teilmenge
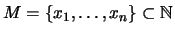 mit
mit 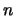 Elementen,
Elementen,
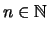 , hat ein Maximum.
, hat ein Maximum.
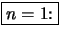
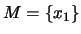 und
und
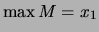 .
.
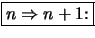
-
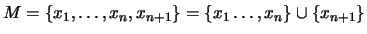 .
Also ist
.
Also ist




Nächste Seite: Kartesisches Produkt
Aufwärts: Abbildungen
Vorherige Seite: Komposition von Abbildungen
Inhalt
Analysis1-A.Lambert
2001-02-09
![]() und
und
![]() eine nichtleeren Teilmenge.
eine nichtleeren Teilmenge.
![]() ,
,
![]() ,
und kürzt den Sachverhalt folgendermaßen ab:
,
und kürzt den Sachverhalt folgendermaßen ab:
![]() heißt die Anzahl der Elemente von
heißt die Anzahl der Elemente von ![]() oder die
Mächtigkeit von
oder die
Mächtigkeit von ![]() .
.
![[*]](crossref.png) ist die Mächtigkeit einer endlichen Menge wohldefiniert.
ist die Mächtigkeit einer endlichen Menge wohldefiniert.
![]() von
von
![]() ,
so daß die andere Aufzählung die Form
,
so daß die andere Aufzählung die Form
![[*]](crossref.png) ist eine Teilmenge
ist eine Teilmenge ![]() ist, so ist
die Mächtigkeit von
ist, so ist
die Mächtigkeit von ![]() kleiner als die Mächtigkeit von
kleiner als die Mächtigkeit von ![]() .
.
![[*]](crossref.png) .
Wir zeigen die folgende Behauptung durch vollständige Induktion:
.
Wir zeigen die folgende Behauptung durch vollständige Induktion:
![]() mit
mit ![]() Elementen,
Elementen,
![]() , hat ein Maximum.
, hat ein Maximum.