![[*]](crossref.png) und erklären das Karthesische Produkt von endlich vielen Mengen:
und erklären das Karthesische Produkt von endlich vielen Mengen:
Wir verallgemeinern die Definition ![[*]](crossref.png) und erklären das Karthesische Produkt von endlich vielen Mengen:
und erklären das Karthesische Produkt von endlich vielen Mengen:
Sind die Mengen
![]() nicht leere Mengen,
dann heißt die Menge
nicht leere Mengen,
dann heißt die Menge
Anmerkung:
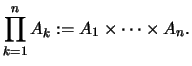
![]() heißt ein Tripel
heißt ein Tripel
![]() heißt ein Quadrupel.
heißt ein Quadrupel.
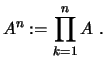
![\begin{displaymath}\{0,1\}^3 =
\begin{array}[t]{l@{}l@{}l}
\{& (0,0,0),\ (0,0,1)...
...\\
& (1,0,0),\ (1,0,1),\ (1,1,0),\ (1,1,1) & \}\ .
\end{array}\end{displaymath}](img418.png) |
Anmerkung: (Abbildungen mit ![]() Variablen)
Variablen)
Abbildungen von einem kartesischen Produktes
![]() in eine Menge
in eine Menge ![]() nennt man auch
Abbildungen mit
nennt man auch
Abbildungen mit ![]() Variablen:
Variablen:
Beispiele sind die Projektionen auf die Kordinaten:
Verknüpfungen sind Abbildungen
![]()
Die Addition ist eine Verküpfung:
Es seien ![]() eine Menge und
eine Menge und
![]() ,
,
![]() , Abbildungen.
Man definiert dann das
, Abbildungen.
Man definiert dann das ![]() -Tupel:
-Tupel:
Beispiel:
Ein Punkt in der Ebene ist durch seine Koordinaten
![]() festgelegt.
Eine zeitliche Bewegung eines Punktes in der Ebene
beschreibt man durch zwei Funktionen
festgelegt.
Eine zeitliche Bewegung eines Punktes in der Ebene
beschreibt man durch zwei Funktionen
Es seien
![]() ,
,
![]() , Abbildungen.
Man definiert das kartesische Produkt der Abbildungen:
, Abbildungen.
Man definiert das kartesische Produkt der Abbildungen:
Beispiel: Ein Tupel von Abbildungen: