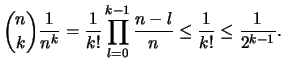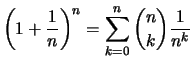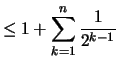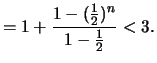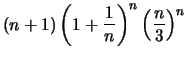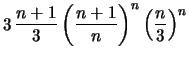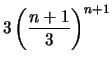Nächste Seite: Approximation der Eulerschen Zahl
Aufwärts: Ungleichungen
Vorherige Seite: Ungleichungen
Inhalt
Bernoullische Ungleichung
Jakob Bernoulli, 1654-1705.
Anmerkung: Zum Beweis unterscheide man die Fälle:
-
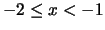 :
:
- klar
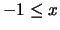 :
:- Vollständige Induktion.
Satz 1.5.2
- Für alle
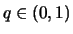 existiert ein
existiert ein 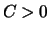 so, daß für alle
so, daß für alle
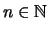 gilt:
gilt:
- Für alle
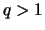 existiert ein
existiert ein 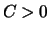 so, daß für alle
so, daß für alle
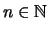 gilt:
gilt:
Hinweis: (1) Man schreibe
und benutze nun die Bernoullische Ungleichung.
Zur Abschätzung der Fakultäten 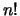 ist es naheliegend die Faktoren durch
ihren ,,Mittelwert``
ist es naheliegend die Faktoren durch
ihren ,,Mittelwert``
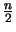 zu ersetzen.
zu ersetzen.
Wir zeigen in den beiden folgenden Sätzen, daß für
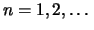
gilt.
Beweis .
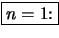
- nachrechnen!
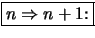
-
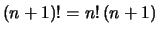 |
| |
|
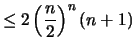 (nach Induktionsvoraussetzung) (nach Induktionsvoraussetzung) |
|
| |
|
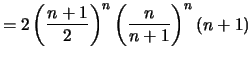 |
|
| |
|
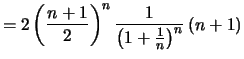 |
|
| |
|
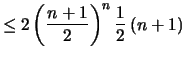 |
|
| |
|
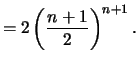 |
|
Beweis . Für
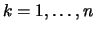 ist
ist
Also
Beweis .
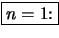
- klar.
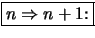
- Die Ungleichung gelte für ein
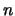 , dann folgt:
, dann folgt:




Nächste Seite: Approximation der Eulerschen Zahl
Aufwärts: Ungleichungen
Vorherige Seite: Ungleichungen
Inhalt
Analysis1-A.Lambert
2001-02-09
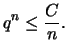

![]() ist es naheliegend die Faktoren durch
ihren ,,Mittelwert``
ist es naheliegend die Faktoren durch
ihren ,,Mittelwert``
![]() zu ersetzen.
zu ersetzen.
![]()
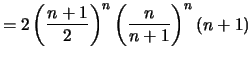
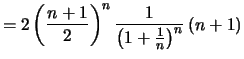
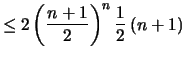
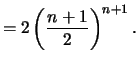
![]() ist
ist