|
( |
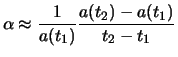
Diskrete Simulation eines Wachstumsprozesses.
Man hat die folgende Beobachtung eines realen Prozesses:
|
( |
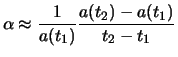
Aufstellung eines diskreten mathematischen Modells
zur Berechnung der zeitlichen Entwicklung für einen größeren
Zeitraum ![]() .
Der Wert
.
Der Wert ![]() sei bekannt.
sei bekannt.
Man wähle eine
![]() und teile das Intervall
und teile das Intervall ![]() in
in ![]() gleiche Teile.
Für die Teilpunkte
gleiche Teile.
Für die Teilpunkte
![]() ,
,
![]() ,
ergibt das Modell die Werte
,
ergibt das Modell die Werte ![]() .
Zur Berechnung der
.
Zur Berechnung der ![]() wende man nacheinander auf die Teilintervalle
die Näherungformel (
wende man nacheinander auf die Teilintervalle
die Näherungformel (![]() ) an.
) an.
Die ![]() kann man rekursiv berechnen. Für
kann man rekursiv berechnen. Für
![]() gilt:
gilt:
| Anfangswert: |
||||
| Rekursion: |
Also ist für
![]() :
:
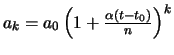
Frage: Wie groß soll man das
![]() wählen und wie ändern sich die
Endwerte
wählen und wie ändern sich die
Endwerte
![]() mit
mit ![]() ?
Zur Vereinfachung betrachten wir vorerst den Fall
?
Zur Vereinfachung betrachten wir vorerst den Fall
![]() .
.
Wir untersuchen nun die Folge
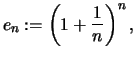
Für die Länge der Intervalle gilt
(vgl.Lemma ![[*]](crossref.png) und
und ![[*]](crossref.png) ):
):
Anmerkung: (Intervallschachtelung für e)
Unsere Anschauung sagt uns, daß die Länge der Intervalle beliebig klein wird. Wenn man diese Begriff ,,beliebig klein werden`` präzisiert, sieht man, daß man dies nicht beweisen kann, sondern als ein Axiom der reellen Zahlen (siehe Archimedisches Axiom) fordern muß.
Wenn wir nun bereits wissen, daß die Intervalle beliebig klein werden, dann sollten sie sich auf einen Punkt zusammenziehen. Wir werden zeigen, daß dieser Punkt keine rationale Zahl sein kann.
Die Existenz einer reellen Zahl, die in allen diesen Intervallen liegt, werden wir später aus einem weiteren Axiom der reellen Zahlen (siehe Intervallschachtelungsprinzip) folgern.
Diese Zahl, die durch die im Satz ![[*]](crossref.png) angegebene
Intervallschachtelung bestimmt wird, heißt die Eulersche Zahl
angegebene
Intervallschachtelung bestimmt wird, heißt die Eulersche Zahl ![]() , nach
Leonhard Euler (1707-1783)
, nach
Leonhard Euler (1707-1783)
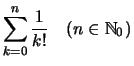
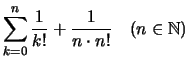
Vergleichen wir diese mit den vorhergehenden Folgen:
Wir setzen zur Abkürzung
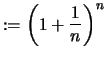 |
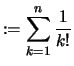 |
|||
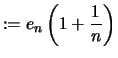 |
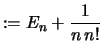 |
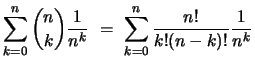 |
|||
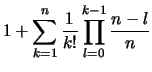 |
|||
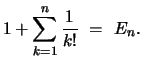 |
(b) Für ![]() gilt
gilt
![]() .
Für
.
Für
![]() gilt:
gilt:
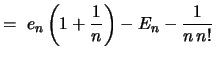 |
||
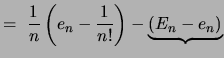 |
||
|
tex2html_deferredDa (siehe nächste Folie) tex2html_wrap_inline$ ( E_n - e_n) &le#leq;1n(E_n-1-12 )$ ist, folgt:
| ||
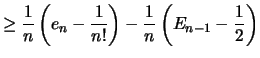 |
||
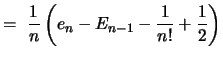 |
||
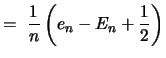 |
||
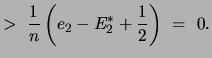 |
||
Hilfsbehauptung
![]() für
für
![]() :
:
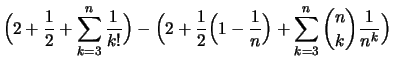 |
(1) | |
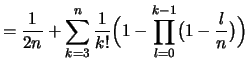 |
(2) | |
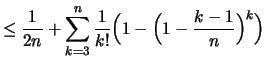 |
(3) | |
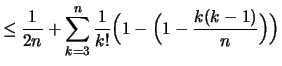 |
(4) | |
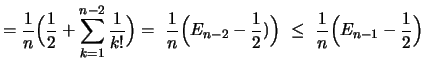 |
Wir verwenden weiterhin die Abkürzungen:
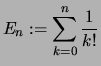 und
und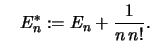
Es gibt keine rationale Zahl, die in allen Intervallen
![]() ,
,
![]() , liegt.
, liegt.
Anmerkung: Der Beweis wird etwas mehr zeigen:
Wenn
![]() ,
,
![]() ,
,
![]() , dann ist
, dann ist
Beweis (e nicht rational).
Annahme: es gibt ein
![]() , so daß gilt:
, so daß gilt:
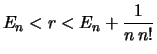
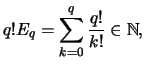 |
|
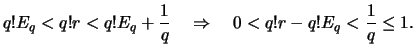 |