



Nächste Seite: Cauchysches Konvergenzkriterium
Aufwärts: Vollständigkeit der reellen Zahlen
Vorherige Seite: Intervallschachtelungen
Inhalt
Um in den reellen Zahlen
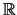 die Existenz der Zahl
die Existenz der Zahl 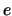 , oder die Existenz der Wurzel aus einer
positiven Zahl zu sichern, brauchen wir ein weiteres Axiom für
, oder die Existenz der Wurzel aus einer
positiven Zahl zu sichern, brauchen wir ein weiteres Axiom für
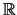 ,
daß die Vollständigkeit von
,
daß die Vollständigkeit von
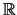 sichert:
sichert:
Definition 2.2.6 (Intervallschachtelungsprinzip)
- (I)
- Es sei
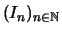 eine Intervallschachtelung in
eine Intervallschachtelung in
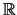 .
Dann existiert ein
.
Dann existiert ein
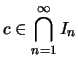 .
.
Bemerkung.
Nach Lemma ![[*]](crossref.png) gibt es genau ein
gibt es genau ein
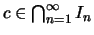 .
.
Anmerkung.
- Ein geordneter Körper, der die Axiome A und I erfüllt, heißt
vollständig geordneter Körper.
- Man kann zeigen, daß es - bis auf Isomorphie - genau einen vollständig
geordneten Körper gibt. Das sind die reellen Zahlen.
- Der Beweis der Existenz und Eindeutigkeit der reellen Zahlen
überfordert den Anfänger und
ist für das weitere Vorgehen erstmal entbehrlich.
Wir werden am Ende Semesters darauf eingehen.
- Die Vorlesung Analysis I handelt davon, welche Folgerungen man
aus den Axiomen eines vollständig geordneten Körpers ziehen kann.
- Es gibt eine Reihe von äquivalenten Forderungen, um die Vollständigkeit
eines geordneten Körpers zu beschreiben.
Die Lehrbücher unterscheiden sich darin, welche der Forderungen sie als
Axiom und welche als Folgerung wählen.
- Andere übliche äquivalente Forderungen sind u.a.
- Cauchysches Konvergenzkriterium
- Supremums-Eigenschaft
- Dedekindsches Schnittaxiom
- Wir werden das Cauchysche Konvergenzkriterium und die
Supremumseigenschaft untersuchen.




Nächste Seite: Cauchysches Konvergenzkriterium
Aufwärts: Vollständigkeit der reellen Zahlen
Vorherige Seite: Intervallschachtelungen
Inhalt
Analysis1-A.Lambert
2001-02-09
![]() die Existenz der Zahl
die Existenz der Zahl ![]() , oder die Existenz der Wurzel aus einer
positiven Zahl zu sichern, brauchen wir ein weiteres Axiom für
, oder die Existenz der Wurzel aus einer
positiven Zahl zu sichern, brauchen wir ein weiteres Axiom für
![]() ,
daß die Vollständigkeit von
,
daß die Vollständigkeit von
![]() sichert:
sichert:
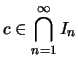 .
.![[*]](crossref.png) gibt es genau ein
gibt es genau ein
![]() .
.