



Nächste Seite: Vollständig geordneter Körper
Aufwärts: Vollständigkeit der reellen Zahlen
Vorherige Seite: Vollständigkeit der reellen Zahlen
Inhalt
Bezeichnung 2.2.1
Ein Intervall
![$ [a,b] $](img882.png)
mit Endpunkten
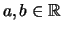
heiße kurz ein
kompaktes Intervall.
Statt kompaktes Intervall sagt man auch abgeschlossenes, beschränktes
Intervall.
Bezeichnung 2.2.2
Eine
Intervallschachtelung ist eine Folge
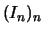
kompakter Intervalle mit den Eigenschaften:
- Für
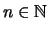 ist
ist
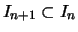 .
.
- Die Längen
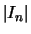 der Intervalle konvergieren gegen Null.
der Intervalle konvergieren gegen Null.
Lemma 2.2.3
Es sei
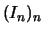
eine Intervallschachtelung. Wenn
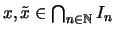
, dann ist
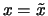
.
Beispiel. Im Abschnitt ![[*]](crossref.png) haben wir die
Intervallschachtelungen
haben wir die
Intervallschachtelungen
konstruiert. Offensichtlich ist die Länge (vgl ![[*]](crossref.png) )
Z. B. für
)
Z. B. für 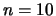 ist die Länge kleiner als
ist die Länge kleiner als
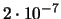 .
.
In Satz ![[*]](crossref.png) haben wir gesehen, daß es keine
rationale Zahl gibt, die in allen Intervallen
haben wir gesehen, daß es keine
rationale Zahl gibt, die in allen Intervallen
![$ [E_n,E_n^*]$](img668.png) ,
,
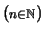 ,
liegt.
,
liegt.
Wir werden die Existenz einer Zahl 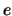 , die in allen Intervallen
, die in allen Intervallen
![$ [E_n,E_n^*]$](img668.png) liegt, aus einem weiteren Axiom (
liegt, aus einem weiteren Axiom (![[*]](crossref.png) ) folgern.
) folgern.
Bemerkung 2.2.4 (Wurzel aus
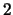
ist nicht rational)
|
Es gibt keine rationale Zahl
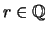 mit
mit 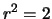 .
.
Beweis . Es sei
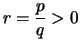 ,
,
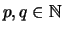 , so daß
, so daß 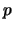 und
und 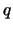 keinen gemeinsamen Teiler haben.
Aus
keinen gemeinsamen Teiler haben.
Aus
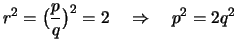 .
.
Also ist 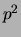 eine gerade Zahl und somit muß auch
eine gerade Zahl und somit muß auch 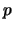 gerade sein.
Es gilt
gerade sein.
Es gilt 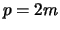 mit einem
mit einem
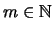 .
Es folgt:
.
Es folgt:
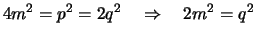 .
.
Also ist auch 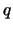 eine gerade Zahl und
eine gerade Zahl und 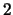 ist ein gemeinsamer Teiler
von
ist ein gemeinsamer Teiler
von 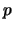 und
und 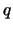 . Widerspruch!
Wir konstruieren eine Intervallschachtelung zur Bestimmung der Wurzel:
. Widerspruch!
Wir konstruieren eine Intervallschachtelung zur Bestimmung der Wurzel:
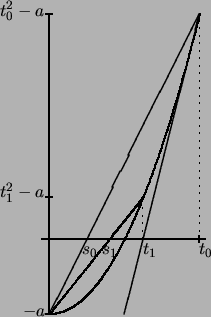
Beispiele 2.2.5 (Intervallschachtelung: Wurzel)
Es sei
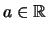 ,
, 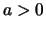 . Wir definieren rekursiv eine Folge
. Wir definieren rekursiv eine Folge 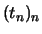 :
:
| |
Anfangswert: |
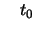 |
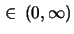 |
|
beliebig |
|
| |
Rekursion: |
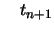 |
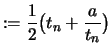 |
|
für
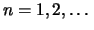 |
|
Für
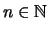 gilt
gilt 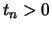 und
und
Die Folge
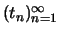
ist monoton fallend:
Da die Folge
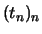
monoton und beschränkt ist, folgt nach
Korollar
![[*]](crossref.png)
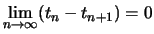 .
.
Wir bilden eine zweite, monoton wachsende Folge
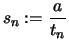 ,
,
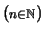 .
Aus
.
Aus
folgt für alle
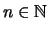
:
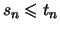 und
und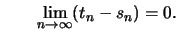
Wir haben also eine Intervallschachtelung
![$ [s_n,t_n] $](img929.png)
,
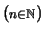
.
Diese Intervallschachtelung definiert die positive Wurzel aus 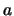 , denn
es gilt:
, denn
es gilt:
![$\displaystyle x \in \bigcap_{n\in\mathbb{N}} [s_n,t_n] \quad\iff\quad x^2 = a$](img930.png) .
.
- Für
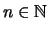 folgt aus
folgt aus
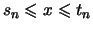 , daß:
, daß:
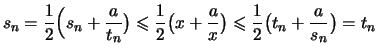 .
.
Nach Lemma
![[*]](crossref.png) ist
ist
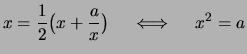 .
.

- Es sei
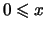 und
und 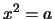 . Für
. Für
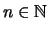 folgt
aus (
folgt
aus (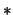 ):
):
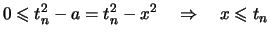 .
.
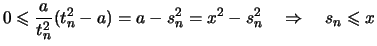 .
.




Nächste Seite: Vollständig geordneter Körper
Aufwärts: Vollständigkeit der reellen Zahlen
Vorherige Seite: Vollständigkeit der reellen Zahlen
Inhalt
Analysis1-A.Lambert
2001-02-09
![[*]](crossref.png) haben wir die
Intervallschachtelungen
haben wir die
Intervallschachtelungen
![$\displaystyle [E_n,E_n^*] =
\Bigl[\sum_{k=0}^n\frac{1}{k!},\,\sum_{k=0}^n\frac{1}{k!}+\frac{1}{n\cdot n!}\Bigr]$](img888.png) für
für
![[*]](crossref.png) )
)
![$\displaystyle \left\vert [E_n, E_n^*] \right\vert = \frac{1}{n\cdot n!} <
\frac{1}{9}\bigl(\frac{3}{n}\bigr)^{n+1}.
$](img889.png)
![[*]](crossref.png) haben wir gesehen, daß es keine
rationale Zahl gibt, die in allen Intervallen
haben wir gesehen, daß es keine
rationale Zahl gibt, die in allen Intervallen
![]() ,
,
![]() ,
liegt.
,
liegt.
![]() , die in allen Intervallen
, die in allen Intervallen
![]() liegt, aus einem weiteren Axiom (
liegt, aus einem weiteren Axiom (![[*]](crossref.png) ) folgern.
) folgern.
![]() ,
,
![]() , so daß
, so daß ![]() und
und ![]() keinen gemeinsamen Teiler haben.
Aus
keinen gemeinsamen Teiler haben.
Aus
![]() ,
, ![]() . Wir definieren rekursiv eine Folge
. Wir definieren rekursiv eine Folge ![]() :
:
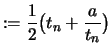
![]() gilt
gilt ![]() und
und
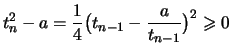 . (
. (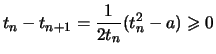 für
für
![[*]](crossref.png)
![]() ,
,
![]() .
Aus
.
Aus
![]() , denn
es gilt:
, denn
es gilt:
![$\displaystyle x \in \bigcap_{n\in\mathbb{N}} [s_n,t_n] \quad\iff\quad x^2 = a$](img930.png) .
.