



Nächste Seite: Geordnete Körper
Aufwärts: Reelle Zahlen
Vorherige Seite: Reelle Zahlen
Inhalt
Die Menge
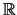 genügt den Körperaxiomen:
genügt den Körperaxiomen:
Definition 1.1.2 (Körperaxiome.)
- (K1)
- Je zwei Elementen
 ,
,
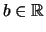 ist eindeutig ein Element
ist eindeutig ein Element
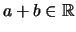 zugeordnet, das Summe von
zugeordnet, das Summe von  und
und 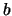 heißt.
heißt.
- (K2)
- Für
 ,
, 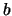 ,
,
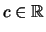 gilt das Assoziativgesetz
gilt das Assoziativgesetz
- (K3)
- Es gibt ein Element
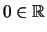 , so daß für alle
, so daß für alle
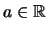 gilt
gilt
- (K4)
- Zu
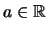 gibt es
gibt es
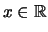 mit
mit 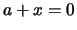 .
.
- (K5)
- Für
 ,
,
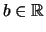 gilt das Kommutativgesetz
gilt das Kommutativgesetz
- (K6)
- Für
 ,
,
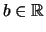 ist eindeutig ein Element
ist eindeutig ein Element
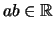 zugeordnet,
das Produkt von
zugeordnet,
das Produkt von  und
und 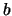 heißt.
heißt.
- (K7)
- Für
 ,
, 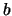 ,
,
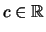 gilt das Assoziativgesetz
gilt das Assoziativgesetz
- (K8)
- Es gibt ein Element
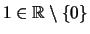 ,
so daß für alle
,
so daß für alle
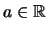 gilt
gilt
- (K9)
- Zu
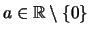 gibt es
gibt es
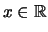 mit
mit 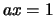 .
.
- (K10)
- Für
 ,
,
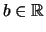 gilt das Kommutativgesetz
gilt das Kommutativgesetz
- (K11)
- Für
 ,
, 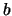 ,
,
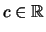 gilt das Distributivgesetz
gilt das Distributivgesetz
Eine Menge mit den Eigenschaften (K1) - (K11) heißt ein Körper.
Außer den reellen Zahlen gibt es noch viele weitere Körper,
die zum Teil ganz andere Eigenschaften haben:
Bemerkung 1.1.4
- Aus den Körperaxiomen folgen alle weiteren bekannten Rechenregeln
für Addition, Subtraktion, Multiplikation und Division von Zahlen.
- Die Lösung der Gleichung (K3)
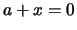 ist eindeutig.
Wir nennen die Lösung den negativen Wert von
ist eindeutig.
Wir nennen die Lösung den negativen Wert von  und bezeichnen sie mit
und bezeichnen sie mit 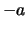 .
Differenzen definieren wir wie üblich als
.
Differenzen definieren wir wie üblich als
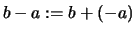 .
.
- Die Lösung der Gleichung (K9)
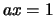 ist eindeutig.
Wir nennen die Lösung den Kehrwert von
ist eindeutig.
Wir nennen die Lösung den Kehrwert von  und bezeichnen sie mit
und bezeichnen sie mit
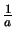 .
Brüche definieren wir wie üblich
.
Brüche definieren wir wie üblich
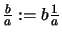 .
.
- Wir benutzen die Potenzschreibweise
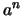 für das
für das 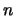 -fache Produkt
von
-fache Produkt
von  mit sich, setzen
mit sich, setzen
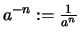 und verwenden die bekannten Rechenregeln für ganzzahlige Potenzen.
Insbesondere setzen wir
und verwenden die bekannten Rechenregeln für ganzzahlige Potenzen.
Insbesondere setzen wir 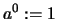 für alle
für alle
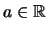 .
.




Nächste Seite: Geordnete Körper
Aufwärts: Reelle Zahlen
Vorherige Seite: Reelle Zahlen
Inhalt
Analysis1-A.Lambert
2001-02-09
![]() genügt den Körperaxiomen:
genügt den Körperaxiomen:
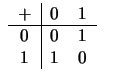
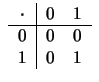
![]() gilt
gilt ![]() .
.