- (O1)
- Es gibt eine
Teilmenge
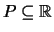 , so daß für alle
, so daß für alle
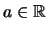 genau eine der
folgenden drei Möglichkeiten zutrifft:
genau eine der
folgenden drei Möglichkeiten zutrifft:
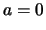 ,
,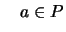 ,
,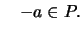
- (O2)
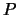 ist abgeschlossen unter der Addition, d.h. für
ist abgeschlossen unter der Addition, d.h. für
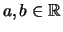 gilt
gilt 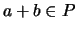 .
.
- (O3)
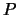 ist abgeschlossen unter der Multiplikation, d.h. für
ist abgeschlossen unter der Multiplikation, d.h. für 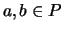 gilt
gilt 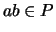 .
.
Bezeichnung Wir werden später die Menge der positiven reellen Zahlen mit
![]() bezeichnen oder als offenes Intervall
bezeichnen oder als offenes Intervall
![]() schreiben.
schreiben.
Ein Körper, der die Ordnungsaxiome (O1) - (O3) erfüllt, heißt ein geordneter Körper.