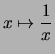 .
.
- Für die Inversion
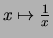 existiert der Grenzwert im Punkte
existiert der Grenzwert im Punkte 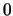 nicht.
nicht.
- Für Folgen
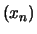 in
in
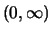 mit
mit
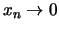 gilt
gilt
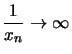 .
.
- Für Folgen
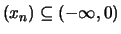 mit
mit
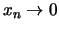 gilt
gilt
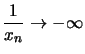 .
.
- Strebt
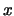 gegen
gegen 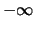 oder
oder 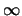 so strebt
so strebt
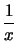 gegen 0.
gegen 0.
D.h. für jede Folge
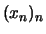 mit
mit
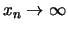 oder
oder
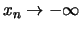 gilt
gilt
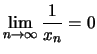 .
.
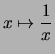 .
.
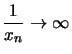 .
.
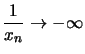 .
.
D.h. für jede Folge ![]() mit
mit
![]() oder
oder
![]() gilt
gilt
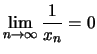 .
.
Wir wollen also noch Grenzwerte für
![]() einführen
und den Fall
einführen
und den Fall
![]() betrachten.
betrachten.
Wir geben eine Definition des Grenzwertes auf offenen Intervallen, die diese Fälle und die vorangehenden umfaßt:
Gegeben seien:
Die Funktion ![]() strebt gegen
strebt gegen ![]() für
für
![]() , falls für jede Folge
, falls für jede Folge ![]() in
in
![]() aus
aus
![]() stets
stets
![]() folgt.
folgt.
Bezeichnung.
Wir schreiben für obige Definition:
![]() oder
oder
![]() für
für ![]() .
.
Bemerkung. Diese Definition umfaßt die folgenden fünf Fälle
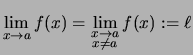 .
.
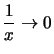 |
für |
|||
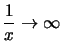 |
für |
|||
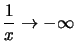 |
für |
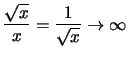 für
für
Gegeben seien:
ein nichtleeres, offenes Intervall, ein
, so daß es eine Folge
in
gibt, die gegen
konvergiert, und eine Funktion
. Also
.
Die folgenden Aussagen sind äquivalent:
Beweis . ![]() Wir führen einen Widerspruchsbeweis.
Wir führen einen Widerspruchsbeweis.
Annahme: Es gilt
![]() für
für ![]() und 2.) gelte nicht.
und 2.) gelte nicht.
Die Folge ![]() konvergiert gegen
konvergiert gegen ![]() und die Folge
und die Folge
![]() ist beschränkt.
ist beschränkt.
Dies ist ein Widerspruch zur Voraussetzung
![]() .
.
Die Folge
![]() und die Folge
und die Folge
![]() ist beschränkt.
ist beschränkt.
Dies ist ein Widerspruch zur Voraussetzung
![]() .
.
![]() Es sei
Es sei ![]() eine Folge in
eine Folge in ![]() mit
mit ![]() .
.
Die Feststellungen
![[*]](crossref.png) gelten sinngemäß für die obigen
Situationen.
gelten sinngemäß für die obigen
Situationen.
Gegeben seien:
ein nichtleeres, offenes Intervall, ein
, so daß es eine Folge
in
gibt, die gegen
konvergiert, und Funktionen
,
mit Grenzwerten
,
.
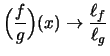 .
.