



Nächste Seite: Komposition von Grenzwerten
Aufwärts: Grenzwerte von Funktionen und
Vorherige Seite: Uneigentliche Grenzwerte
Inhalt
Aus dem Cauchyschen Konvergenzkriterium für Folgen erhält man das
entsprechende Kriterium für Grenzwerte von Funktionen:
Bemerkung.
- Ein entsprechende Kriterien gilt für Grenzwerte
in einem inneren Punkt
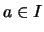 :
:
- Im Fall
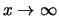 lautet das Cauchy-Kriterium:
lautet das Cauchy-Kriterium:
Beweis .
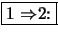 Es sei
Es sei
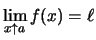 .
Nach Satz
.
Nach Satz ![[*]](crossref.png) gibt es zu
gibt es zu
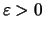 ein
ein 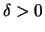 , so daß aus
, so daß aus
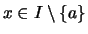 ,
,
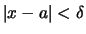 stets
stets
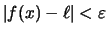 folgt.
Also gilt
für
folgt.
Also gilt
für 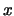 ,
,
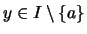 mit
mit
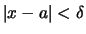 ,
,
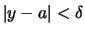
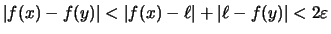 .
.
 Aus 2.) folgt, daß für jede Folge
Aus 2.) folgt, daß für jede Folge  in
in 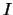 mit Grenzwert
mit Grenzwert
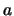 die Folge
die Folge
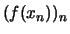 eine Cauchy-Folge ist
und folglich konvergiert.
Nach dem
Reißverschlußprinzip
eine Cauchy-Folge ist
und folglich konvergiert.
Nach dem
Reißverschlußprinzip ![[*]](crossref.png) haben alle diese Folgen den gleichen Grenzwert.
Also exisitiert
haben alle diese Folgen den gleichen Grenzwert.
Also exisitiert
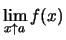 .
.
Bemerkung 2.3.17 (Reißverschlußprinzip)
Wenn 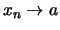 und
und 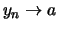 ,
dann konvergiert auch die Folge
,
dann konvergiert auch die Folge
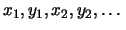 gegen
gegen 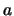 .
Wenn
.
Wenn
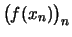 und
und
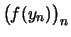 konvergieren,
so konvergiert auch die Folge
konvergieren,
so konvergiert auch die Folge
Somit haben die Folgen
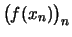
und
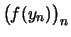
den gleichen Grenzwert.
Satz 2.3.18
Es seien
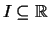
ein nichtleeres, offenes Intervall mit
rechtem Endpunkt
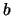
und
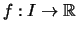
monoton wachsend und beschränkt.
Dann existiert
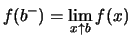
in
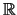
.
Beweis . Annahme: die Cauchy-Bedingung ist nicht erfüllt.
Dann gibt es ein
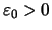 , so daß es zu jedem
, so daß es zu jedem 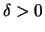 zwei Punkte
zwei Punkte
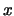 ,
, 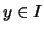 gibt
mit
gibt
mit 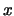 ,
,
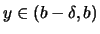 und
und
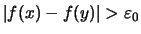 .
.
Zu den Werten
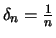 bilde man induktiv zwei
Folgen
bilde man induktiv zwei
Folgen 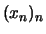 ,
, 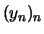 , so daß
, so daß
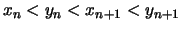 und
und
Dann folgt
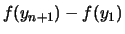
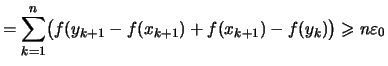 .
.
Die Folge
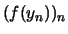 ist also unbeschränkt.
Widerspruch.
ist also unbeschränkt.
Widerspruch.
Bemerkung Wenn
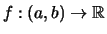 monoton wachsend ist, so gilt:
monoton wachsend ist, so gilt:




Nächste Seite: Komposition von Grenzwerten
Aufwärts: Grenzwerte von Funktionen und
Vorherige Seite: Uneigentliche Grenzwerte
Inhalt
Analysis1-A.Lambert
2001-02-09
![]() mit rechtem
Endpunkt
mit rechtem
Endpunkt
![]() und eine Funktion
und eine Funktion
![]() .
Die folgenden Aussagen sind äquivalent:
.
Die folgenden Aussagen sind äquivalent:
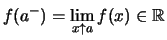 .
.
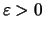 existiert ein
existiert ein
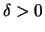 ,
so daß für alle
,
so daß für alle 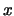 ,
,
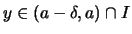 stets
stets
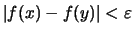 gilt.
gilt.
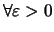

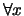 ,
,
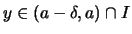
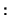
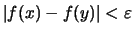 .
.
![[*]](crossref.png)
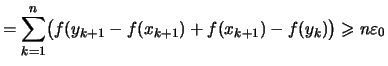 .
.