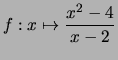
Genauer gilt für jede Folge
![]() in
in
![]() :
:
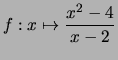
Genauer gilt für jede Folge
![]() in
in
![]() :
:
Bei der Definition des Grenzwertes einer Funktion ![]() in einem Punkt
in einem Punkt ![]() untersuchen wir zunächst den wichtigen Spezialfall, daß der Punkt
untersuchen wir zunächst den wichtigen Spezialfall, daß der Punkt ![]() nicht zum Definitionsbereich von
nicht zum Definitionsbereich von ![]() gehört:
gehört:
Gegeben sei ein offenes Intervall
![]() ,
, ![]() und eine
Funktion
und eine
Funktion
![]() .
.
Eine Zahl
![]() heißt Grenzwert der Funktion
heißt Grenzwert der Funktion ![]() im Punkte
im Punkte ![]() , falls für jede Folge
, falls für jede Folge
![]() in
in
![]() aus
aus
![]() stets
stets
![]() folgt.
folgt.
Bezeichnung. Man schreibt
![]() oder
oder
![]() für
für
![]() .
.
Bemerkung
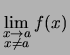 .
.Wir beschränken uns vorerst auf die Fälle, in denen der Unterschied sich nicht bemerkbar macht.
Bemerkung Teil 2.) der Feststellung besagt, daß der Grenzwert nur
vom Verhalten der Funktion
in einer kleinen Umgebung ![]() des Punktes
des Punktes ![]() abhängt.
abhängt.
![]() ist ein offenes Intervall.
ist ein offenes Intervall.
Wir schreiben
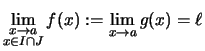 .
.
Setzen
wir diese Funktion in ![]() durch ein beliebiges
durch ein beliebiges
![]() zu einer
auf ganz
zu einer
auf ganz
![]() definierten Funktion fort:
definierten Funktion fort:
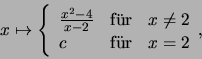
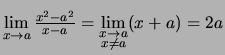 .
.
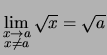 .
.
Für die auf
![]() erklärte Funktion erhält man:
erklärte Funktion erhält man:
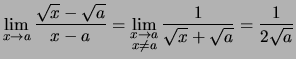 .
.
Die folgende Feststellung liefert eine äquivalente Formulierung der Grenzwertdefinition.
Gegeben sei ein offenes Intervall
![]() ,
, ![]() und eine
Funktion
und eine
Funktion
![]() .
.
Für
![]() sind die folgenden Aussagen äquivalent:
sind die folgenden Aussagen äquivalent:
Bild.
Das heißt, zu jedem
![]() -Intervall
-Intervall
![]() mit Mittelpunkt
mit Mittelpunkt ![]() gibt es ein
gibt es ein ![]() -Intervall
-Intervall
![]() mit Mittelpunkt
mit Mittelpunkt ![]() , so daß
, so daß
Gegeben sei ein offenes Intervall
![]() ,
, ![]() und
Funktionen
und
Funktionen
![]() mit
mit
![]() und
und
![]()
Dann folgt
Auf
![]() gilt dann:
gilt dann:
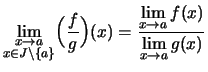
Bezeichnung Im allgemeinen geben wir in der Aussage 3.)
das Intervall ![]() nicht an
und schreiben:
nicht an
und schreiben:
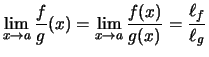 .
.
Wenn
![]() , dann ist
, dann ist
![]() .
.
Wenn
![]() ,
, ![]() beschränkt, dann
beschränkt, dann
![]() .
.
![$\displaystyle \lim\limits_{x\to a}\sqrt[\uproot{2}p]{\strut f(x)}
= \sqrt[\uproot{2}p]{\strut\lim\limits_{x\to a}f(x)}$](img1150.png) .
.
![[*]](crossref.png) für Grenzwerte von Folgen.
für Grenzwerte von Folgen.
Nach Feststellung ![[*]](crossref.png) gibt es zu
gibt es zu
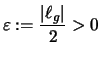 ein
ein ![]() , so daß
für
, so daß
für ![]() und
und
![]() folgendes gilt:
folgendes gilt:
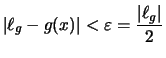 |
|
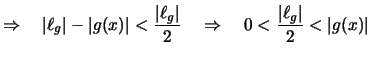 |
![[*]](crossref.png) (3) für Quotienten von Folgen.
(3) für Quotienten von Folgen.
Beispiel.
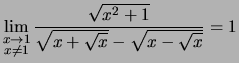
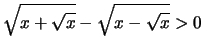 für
für
Es sei ![]() eine Folge mit
eine Folge mit ![]() für
für
![]() .
Dann gilt
.
Dann gilt
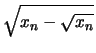 |
||
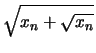 |
||
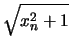 |
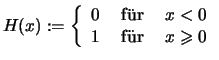
Der Grenzwert
![]() existiert offenbar nicht.
existiert offenbar nicht.
Für Folgen ![]() in
in
![]() mit
mit
![]() gilt
gilt
![]() , für Folgen
, für Folgen ![]() in
in
![]() mit
mit
![]() gilt
gilt
![]() .
.
Man kann daher ![]() als rechtsseitigen Grenzwert
und 0 als linksseitigen Grenzwert von
als rechtsseitigen Grenzwert
und 0 als linksseitigen Grenzwert von ![]() in Punkte 0 auffassen.
in Punkte 0 auffassen.
Gegeben sei ein nichtleeres, offenes Intervall
![]() , mit linkem
Endpunkt
, mit linkem
Endpunkt
![]() und eine Funktion
und eine Funktion
![]() .
.
Eine Zahl
![]() heißt rechsseitiger Grenzwert der Funktion
heißt rechsseitiger Grenzwert der Funktion ![]() im Punkte
im Punkte ![]() , falls für jede Folge
, falls für jede Folge
![]() in
in ![]() aus
aus
![]() stets
stets
![]() folgt.
folgt.
![[*]](crossref.png) .
Man kann also auch
.
Man kann also auch
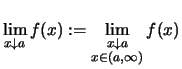 ,
,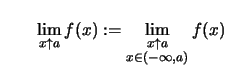 .
. und
und