Gegeben seien:
- (i)
- nichtleere, offene Intervalle
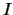 ,
,
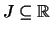 ,
,
- (ii)
- ein
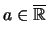 ,
so daß es eine Folge
,
so daß es eine Folge 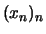 in
in
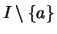 gibt,
die gegen
gibt,
die gegen  konvergiert,
konvergiert,
- (iii)
- eine Funktion
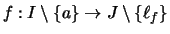 mit Grenzwert
mit Grenzwert
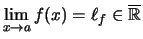
- (iv)
- eine Funktion
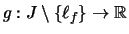 mit Grenzwert
mit Grenzwert
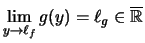 .
.
Gegeben seien:
Wenn
![]() , so muß man eine stärkere Forderung
an die Funktion
, so muß man eine stärkere Forderung
an die Funktion ![]() stellen: (Man zeichne ein Bild!)
stellen: (Man zeichne ein Bild!)
Gegeben seien:
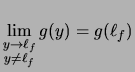 .
.
Beweis . Zu
![]() gibt es ein
gibt es ein ![]() , so daß für alle
, so daß für alle
![]() gilt:
gilt:
Also gilt für jede Folge ![]() in
in ![]() :
:
Bemerkung. Eine Funktion, die die Bedingung (iv) des Lemmas erfült,
wird stetig im Punkte ![]() genannt.
genannt.