Nächste Seite: Allgemeine Grenzwertdefinition
Aufwärts: Grenzwerte von Funktionen und
Vorherige Seite: Komposition von Grenzwerten
Inhalt
Funktionen deren Grenzwerte in einem Punkt stets mit den Funktionswerten
in diesem Punkt übereinstimmen, sind in der Analysis von besonderer
Bedeutung.
Bemerkung.
- Für ein offenes Intervall
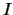 heißt
heißt
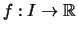
- rechtsseitig stetig in
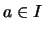 ,
falls
,
falls
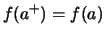 gilt.
gilt.
- linksseitig stetig in
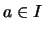 ,
falls
,
falls
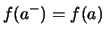 gilt.
gilt.
- Die Stetigkeit einer Funktion kann von der Wahl des
Definitionsbereichs abhängen.
So gilt für die Einschränkungen Heaviside-Funktion
-
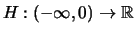 und
und
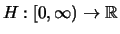 sind stetig.
sind stetig.
-
![$ H:(-\infty,0]\rightarrow \mathbb{R}$](img1333.png) ist nicht stetig.
ist nicht stetig.
-
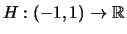 ist in 0 rechtseitig stetig.
ist in 0 rechtseitig stetig.
- Für Intervalle
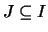 nennt man eine Funktion
nennt man eine Funktion
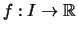 stetig auf
stetig auf
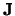 , wenn ihre Einschränkung
, wenn ihre Einschränkung
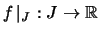 stetig ist.
In diesem Sinne ist die Heaviside-Funktion
stetig ist.
In diesem Sinne ist die Heaviside-Funktion
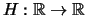 stetig auf
stetig auf ![$ J=[0,1]$](img1339.png) .
.
Bemerkung. Damit kann für in  stetige Funktionen der Funktionswert
stetige Funktionen der Funktionswert 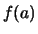 mit Hilfe von Werten
mit Hilfe von Werten 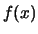 , mit
, mit 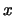 nahe an
nahe an  , angenähert werden.
Die
, angenähert werden.
Die
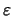 -
-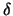 Beziehung gibt Auskunft über die Güte
dieser Approximation.
Beziehung gibt Auskunft über die Güte
dieser Approximation.
Feststellung 2.3.24 (Rechenregeln: stetige Funktionen)
Es seien
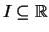
ein Intervall und
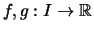
in
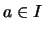
stetig und
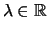
.
Dann sind auch auch die folgenden Funktionen in

stetig:
und, wenn
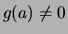
,
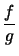 .
.
Bemerkung. Der Quotient
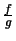 ist stetig auf der Menge
ist stetig auf der Menge
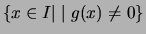 .
.
Satz 2.3.25 (Komposition stetiger Funktionen)
Es seien
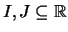
Intervalle und
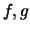
Funktionen mit:
Wenn
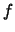
stetig in
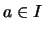
und
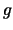
stetig in
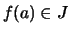
,
dann ist
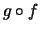
stetig in

.
Beispiele 2.3.26
- Für
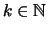 ist
ist
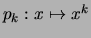 stetig auf
stetig auf
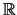 .
.
- Für
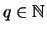 ist nach Feststellung
ist nach Feststellung ![[*]](crossref.png)
![$ \sqrt[\uproot{2}q]{\rule{0pt}{1ex}~} : x \mapsto \sqrt[\uproot{2}q]{x} $](img1357.png) stetig auf
stetig auf
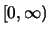 .
.
- Für
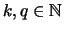 ist
ist
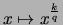 stetig auf
stetig auf
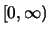 .
.




Nächste Seite: Allgemeine Grenzwertdefinition
Aufwärts: Grenzwerte von Funktionen und
Vorherige Seite: Komposition von Grenzwerten
Inhalt
Analysis1-A.Lambert
2001-02-09
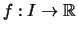 heißt stetig in einem Punkt
heißt stetig in einem Punkt
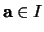 ,
falls
,
falls 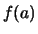 der Limes von
der Limes von 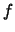 in
in  bezüglich
bezüglich 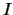 ist.
ist.
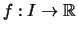 heißt stetig (auf I),
falls
heißt stetig (auf I),
falls 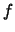 in jedem Punkt von
in jedem Punkt von 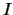 stetig ist.
stetig ist.
![]() ist stetig auf der Menge
ist stetig auf der Menge
![]() .
.