



Nächste Seite: Zwischenwertsatz
Aufwärts: Supremum und Zwischenwertsatz
Vorherige Seite: Supremum
Inhalt
Für nach oben unbeschränkte Mengen
führen wir ein uneigentliches Supremum in
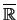 ein.
ein.
Man kann dann gewisse Sachverhalte statt in Worten
kurz in Formeln ausdrücken und kann
mit diesen uneigentlichen Suprema auch rechnen
(vgl. ![[*]](crossref.png) ).
).
Bezeichnung 2.5.9 (
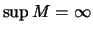
)
Es sei
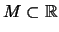 nicht leer.
nicht leer.
- Wenn
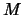 nach oben unbeschränkt ist, setzen wir
nach oben unbeschränkt ist, setzen wir
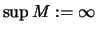 .
.
- Wenn
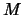 nach unten unbeschränkt ist, setzen wir
nach unten unbeschränkt ist, setzen wir
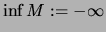 .
.
Beispiele 2.5.10 (
)
Es sei
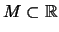 nicht leer. Dann gilt:
nicht leer. Dann gilt:
-
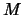 nach oben beschränkt
nach oben beschränkt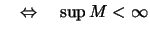
- Mit der Bezeichnung
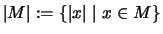 gilt:
gilt:
Beispiele 2.5.11 (Supremum monotoner Folgen)
Es sei 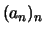 eine monoton wachsende Folge. Dann gilt:
eine monoton wachsende Folge. Dann gilt:
-
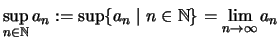 .
.
-
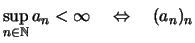 beschränkt.
beschränkt.
Folgerung aus der Existenz von Suprema und Infima:
Beweis .
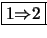
- Für Intervalle gilt offensichtlich (2.)
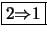
- Setze
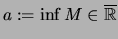 und
und
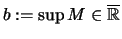 .
.
Wir zeigen zunächst, daß
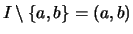 ist:
ist:
Es gibt nun vier Fälle, je nachdem ob  oder
oder 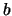 in
in 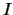 oder nicht in
oder nicht in 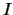 liegen:
liegen:




Nächste Seite: Zwischenwertsatz
Aufwärts: Supremum und Zwischenwertsatz
Vorherige Seite: Supremum
Inhalt
Analysis1-A.Lambert
2001-02-09
![]() ein.
ein.
![[*]](crossref.png) ).
).
![]() nicht leer.
nicht leer.
![]() nicht leer. Dann gilt:
nicht leer. Dann gilt:
![]() eine monoton wachsende Folge. Dann gilt:
eine monoton wachsende Folge. Dann gilt:
![]() nicht leer.
Dann sind äquivalent:
nicht leer.
Dann sind äquivalent:
![]() ist:
ist: