Bemerkung.
Mit dem Integral einer Funktion
![]() auf
einem Intervall
auf
einem Intervall ![]() wird die Fläche angegeben,
die durch das Intervall
wird die Fläche angegeben,
die durch das Intervall ![]() auf der Koordinatenachse
und den Graphen von
auf der Koordinatenachse
und den Graphen von ![]() begrenzt wird.
begrenzt wird.
Dabei zählen Flächen oberhalb der Koordinatenachse positiv und Flächen unterhalb der Korodinatenachse negativ.
Für kompakte Intervalle![]() kann man
den Quotienten aus der obigen Fläche und der Länge
kann man
den Quotienten aus der obigen Fläche und der Länge ![]() des
Intervalls als Mittelwert der Funktion
des
Intervalls als Mittelwert der Funktion ![]() auf dem
Intervall
auf dem
Intervall ![]() ansehen.
ansehen.
Beispiel aus der Physik:
Wenn das Fahrzeug rückwärts fährt ist ![]() .
.
Bemerkung.
In den Lehrbüchern findet man unterschiedliche Zugänge zum Integral, die sich, abgesehen von den verschiedenen Konstruktionen, darin unterscheiden, wie umfangreich die Funktionenklassen sind, für die ein Integral erklärt wird.
Mit wachsender Allgemeinheit aufgezählt sind dies
Diese Integralbegriffe ergeben auf den jeweils kleineren Funktionenklassen dasselbe Ergebnis.
Bemerkung. Das Ziel der Integraltheorien ist weniger, für möglichst wilde Funktionen ein Integral zu erklären, sondern zu zeigen, wie sich das Integral mit unterschiedlichen Konvergenzbegriffen für Funktionenfolgen verträgt.
Eine Folge von Funktionen kann z. B. beschränkt oder monoton sein und sie kann punktweise oder gleichmäßig gegen eine Grenzfunktion konvergieren.
Die folgenden Regeln sollten so allgemein wie möglich gelten:
Bemerkung (Zur Wahl der Integrationstheorie).
In der Analysis I beschränken wir uns vorerst auf:
Bemerkung Wir charakterisieren das Integral der Regelfunktionen durch Axiome, die durch die anschauliche Deutung des Integrals als Fläche nahegelegt werden:
Das Regel-Integral ist eine Familie von Abbildungen von den Regelfunktionen in die reellen Zahlen mit den folgenden Eigenschaften:
1. Zu jedem nichtleeren, kompakten Intervall
![]() ,
gibt es eine Abbildung, die man
Integral über
,
gibt es eine Abbildung, die man
Integral über ![]() nennt:
nennt:
![$\displaystyle \textstyle
\int\limits_{[a,b]} : {\mathcal R}([a,b]) \rightarrow \mathbb{R}$](img2155.png) .
.![$\displaystyle \textstyle
f \mapsto \int\limits_{[a,b]} f$](img2157.png) .
.![$\displaystyle \textstyle
\int\limits_{[a,b]} f \,+\, \int\limits_{[b,c]} f
= \int\limits_{[a,c]} f$](img2160.png) .
.![$\displaystyle \textstyle
f\leqslant g \quad\Rightarrow\quad
\int\limits_{[a,b]} f \leqslant \int\limits_{[a,b]} g$](img2164.png) .
.![$\displaystyle \textstyle
\int\limits_{[a,b]}\! c = c\cdot (b-a)$](img2166.png) .
.
Sehr suggestiv ist die von von Leibniz eingeführte Bezeichnung des
Integrals mit einer formalen Variablen ![]() und einem Differential
und einem Differential ![]() .
Vorerst ist das Differential nur ein Symbol.
.
Vorerst ist das Differential nur ein Symbol.
Es seien ![]() ein nichtleeres Intervall
und
ein nichtleeres Intervall
und
![]() .
In Differentialschreibweise bezeichnet man das Integral mit:
.
In Differentialschreibweise bezeichnet man das Integral mit:
![$\displaystyle \int_a^b f(x)\,dx :=
\textstyle \int\limits_{[a,b]}\! f$](img2168.png) .
.
Bemerkung.
In dieser Bezeichnung wirken das Integralzeichen ![]() und das Differental
und das Differental ![]() wie eine öffnende und eine
schließende Klammer.
wie eine öffnende und eine
schließende Klammer.
Wie bei einem Summationsindex ist die Bezeichnung der Variablen
unwesentlich:
![]() .
.
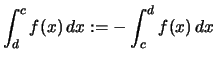 .
.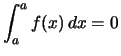 .
.
Bemerkung.
Mit Bezeichnung (1.) gilt für ![]() :
:
Integriert man entlang des Weges von ![]() nach
nach ![]() und dann zurück von
und dann zurück von ![]() nach
nach ![]() , so erhält man das
Integral entlang der Wegstrecke von
, so erhält man das
Integral entlang der Wegstrecke von ![]() nach
nach ![]() .
.
Es seien
![]() ein Intervall
ein Intervall
![]() und
und ![]() . Die Funktion
. Die Funktion
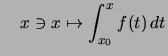
Bemerkung.
![[*]](crossref.png) .
.
Eine Stammfunkton ![]() einer Regelfunktion
einer Regelfunktion
![]() ist
auf jedem kompakten Teilintervall
ist
auf jedem kompakten Teilintervall
![]() Lipschitsstetig.
Lipschitsstetig.
Eine Lipschitzkonstante von ![]() ist
ist
![]() :
:
![$\displaystyle \Bigl\vert \int_a^b f(x)\,dx\, \Bigl\vert \ \leqslant\
\sup\limits_{x\in[a,b]}\!\vert f(x)\vert\ \vert b-a\vert$](img2186.png) .
.
Beweis . Für
![]() gilt
gilt
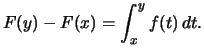
![$\displaystyle = \int\limits_{[x,y]} f\ \leqslant \ $](img2190.png) |
|||||
![$\displaystyle = \int\limits_{[x,y]} f\ \geqslant -$](img2193.png) |