![[*]](crossref.png) axiomatisch festgelegt, welche Eigenschaften
ein Integral hat und einige Folgerungen aus den Axiomen gezogen.
Es ist aber noch unklar, ob es überhaupt
ein Integral für Regelfunktionen gibt und, falls ja, ob es
eindeutig bestimmt ist.
axiomatisch festgelegt, welche Eigenschaften
ein Integral hat und einige Folgerungen aus den Axiomen gezogen.
Es ist aber noch unklar, ob es überhaupt
ein Integral für Regelfunktionen gibt und, falls ja, ob es
eindeutig bestimmt ist.
Bemerkung.
Wir haben in Definiton ![[*]](crossref.png) axiomatisch festgelegt, welche Eigenschaften
ein Integral hat und einige Folgerungen aus den Axiomen gezogen.
Es ist aber noch unklar, ob es überhaupt
ein Integral für Regelfunktionen gibt und, falls ja, ob es
eindeutig bestimmt ist.
axiomatisch festgelegt, welche Eigenschaften
ein Integral hat und einige Folgerungen aus den Axiomen gezogen.
Es ist aber noch unklar, ob es überhaupt
ein Integral für Regelfunktionen gibt und, falls ja, ob es
eindeutig bestimmt ist.
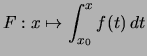
Wir zeigen zuächst, daß das Integral auf den Treppenfunktionen exisitiert und eindeutig erklärt ist.
Bemerkung. Bei der Berechnung des Integral von Treppenfunktionen hilft die folgende Verschärfung der Eichungsvorschrift:
Beweis . Man fixiere ein
![]() . Die Stammfunktion
. Die Stammfunktion
 für
für 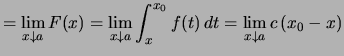 |
||
Subtrahiert man diese beiden Gleichungen, so erhält man
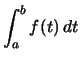 |
||
Bemerkung.
Wir folgern aus den Axiomen ![[*]](crossref.png) für
das Integral eine Formel
für
das Integral eine Formel ![]() für das Integral einer Treppenfunktion
und zeigen anschließend, daß das Integral durch diese Formel
wohldefiniert und damit eindeutig bestimmt ist.
für das Integral einer Treppenfunktion
und zeigen anschließend, daß das Integral durch diese Formel
wohldefiniert und damit eindeutig bestimmt ist.
Es sei ![]() ein kompaktes Intervall,
mit Teilpunkten
ein kompaktes Intervall,
mit Teilpunkten
![]() ,
und
,
und
![]() eine Treppenfunktion,
die auf den Teilintervallen
eine Treppenfunktion,
die auf den Teilintervallen
![]() konstant ist:
konstant ist:
![[*]](crossref.png) muß dann gelten:
muß dann gelten:
![$\displaystyle \textstyle
\int\limits_{[x_{k-1},x_k]}\!\!\! t = c_k(x_k - x_{k-1})$](img2213.png) .
.![$\displaystyle \int\limits_{[a,b]}\!t
\ =\ \sum_{k=1}^n\, \int\limits_{[x_{k-1},x_k]}\!\!\! t
\ =\ \sum_{k=1}^n c_k (x_k - x_{k-1} ) \qquad(\star)$](img2214.png) .
.
Bemerkung.
Die Darstellung einer Treppenfunktion
![]() durch Angabe von Teilpunkten
durch Angabe von Teilpunkten
![]() und der Werte
und der Werte
| für
|
||||
| für
|
Wir wollen zeigen, daß sich das Ergebnis der Formel ![]() von der Darstellung der Treppenfunktion unabhängig ist.
D.h. das Integral ist durch die Formel
von der Darstellung der Treppenfunktion unabhängig ist.
D.h. das Integral ist durch die Formel ![]() wohldefiniert.
wohldefiniert.
Es sei
![]() eine Treppenfunktion.
Wir nennen eine Menge
eine Treppenfunktion.
Wir nennen eine Menge ![]() von Punkten
von Punkten
![]() eine für
eine für ![]() zulässige Zerlegung des
Intervalls
zulässige Zerlegung des
Intervalls ![]() , wenn
, wenn
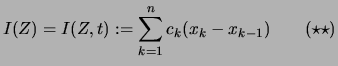 .
.
Bemerkung.
Wir zeigen schreiben später
![]() statt
statt ![]() .
.
Bemerkung.
Wenn ![]() und
und ![]() zulässige Zerlegungungen sind,
so bilde man die Zerlegung
zulässige Zerlegungungen sind,
so bilde man die Zerlegung
![]() , die gerade
aus allen Teilpunkten von
, die gerade
aus allen Teilpunkten von ![]() und den Teilpunkten von
und den Teilpunkten von
![]() besteht, und zeige
besteht, und zeige
Es reicht also zu zeigen, daß beim Hinzufügen eines
weiteren Teilpunktes sich das Ergebnis der Formel
![]() nicht ändert.
nicht ändert.
Dann folgt induktiv
![]() und analog
und analog
![]() .
.
Beweis . Es reicht zu zeigen, daß sich die Zerlegungsumme beim Hinzufügen eines weiteren Teilpunktes nicht ändert.
Es sei
![]() eine
für
eine
für ![]() zulässige Zerlegungen von
zulässige Zerlegungen von ![]() mit
mit
Es gibt ein
![]() ,
so daß
,
so daß
![]() ist. Dann folgt
ist. Dann folgt
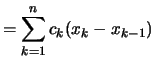 |
||
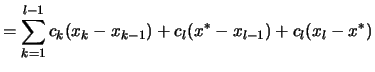 |
||
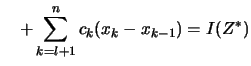 |
Es sei
![]() ein kompaktes Intervall.
Das Integral einer Treppenfunktion
ein kompaktes Intervall.
Das Integral einer Treppenfunktion
![]() definiert man als Zerlegungssumme
zu einer zulässigen Zerlegung
definiert man als Zerlegungssumme
zu einer zulässigen Zerlegung ![]() von
von ![]() (vgl. Bezeichnung
(vgl. Bezeichnung ![[*]](crossref.png) ):
):
Das Integral von Treppenfunktionen erfült die Regeln
![[*]](crossref.png) für ein Integral gefordert
werden. Es ist durch diese Eigenschaften eindeutig bestimmt.
für ein Integral gefordert
werden. Es ist durch diese Eigenschaften eindeutig bestimmt.
Beweis .
![[*]](crossref.png)
![$\displaystyle \textstyle
\int\limits_{[a,b]}\! t \,+\, \int\limits_{[b,c]}\! t
= I(Z_1,t)+I(Z_2,t) = I(Z,t)
= \int\limits_{[a,c]}\! t$](img2248.png) .
.![[*]](crossref.png)
Das Integral von Treppenfunktionen ist linear:
Für Treppenfunktionen ![]() ,
,
![]() und
und ![]() ,
,
![]() gilt
gilt
Beweis . Zu zwei Treppenfunktionen ![]() auf I gibt es eine
gemeinsame zulässige Zerlegung des komapkten Intervalls
auf I gibt es eine
gemeinsame zulässige Zerlegung des komapkten Intervalls ![]() .
Aus der Formel
.
Aus der Formel ![[*]](crossref.png)
![]() folgt
folgt
Bemerkung. Aus der Abschätzung
Es sei
![]() ein kompaktes Intervall.
Für das Integral einer Treppenfunktion
ein kompaktes Intervall.
Für das Integral einer Treppenfunktion
![]() gilt:
gilt:
Bemerkung. Aus der Normabschätzung des Integrals und der Linearität des Integrals erhält man für die Differenz der Integrale zwei Treppenfunktionen die folgende Abschätzung
Es sei
![]() ein kompaktes Intervall.
Für das Integral zweier Treppenfunktionen
ein kompaktes Intervall.
Für das Integral zweier Treppenfunktionen
![]() ,
,
![]() gilt:
gilt:
![$\displaystyle \textstyle
\Bigl\vert\, \int\limits_{[a,b]} t_1 - \int\limits_{[a,b]}t_2 \Bigr\vert
\leqslant (b-a)\,\Vert t_1-t_2 \Vert$](img2259.png) .
.Bemerkung. Diese Ungleichung hat die Form einer Lipschitz-Bedingung und wird genau so benutzt, um die Konvergenz von Integralen zu zeigen.