




Next: cross norms
Up: Tensor Products
Previous: Tensor Products
Contents
Index
Operator space tensor products
An operator space tensor product is the completion of the algebraic tensor
product with respect to an operator space tensor norm.
An
operator space tensor norm
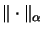 is defined for each pair
is defined for each pair
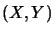 of operator spaces and endows
their algebraic tensor product
of operator spaces and endows
their algebraic tensor product
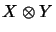 with the structure of an
matrix normed space
with the structure of an
matrix normed space
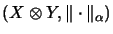 thuch that the following two properties
thuch that the following two properties
![[*]](crossref.png) and
and
![[*]](crossref.png) [BP91, Def. 5.9].
hold.
[BP91, Def. 5.9].
hold.
The completion is called the
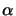 -operator space tensor product
of
-operator space tensor product
of
 and
and
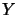 and is denoted by
and is denoted by
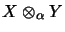 .
.
- 1.
- For the complex numbers holds
- 2.
-
For all
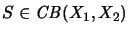 and
and
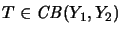 the operator
the operator
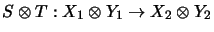 has a continuous extension
The bilinear mapping
has a continuous extension
The bilinear mapping
is
jointly completely contractive .30
- Property
![[*]](crossref.png) may be replaced by the assumptions
may be replaced by the assumptions
![[*]](crossref.png) and
and
![[*]](crossref.png) .31
.31
- 3.
- An operator space tensor product
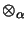 is functorial:
For all
is functorial:
For all
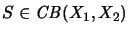 and
and
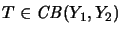 the operator
the operator
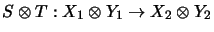 has a continuous extension
and
has a continuous extension
and
- Remark: This is indeed an equality
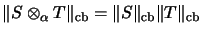 .
.
- 4.
- The algebraic
shuffle isomorphism
 has a continuous extension to a complete contraction:
This complete contraction is called the
shuffle map of the
has a continuous extension to a complete contraction:
This complete contraction is called the
shuffle map of the
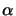 -operator space tensor product.
-operator space tensor product.
Condition ![[*]](crossref.png) is equivalent to the following two
conditions: The
shuffle mappings
is equivalent to the following two
conditions: The
shuffle mappings
are completely contractive.
Operator space tensor producte
may have further special properties:
- An operator space tensor product
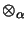 is called
is called
-
symmetric,
if
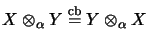 is a complete isometry;
is a complete isometry;
-
associative,
if
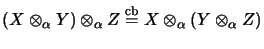 is acomplete isometry;
is acomplete isometry;
-
injective,
if for all subspaces
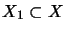 ,
,
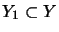 the map
the map
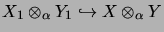 is acomplete isometry;
is acomplete isometry;
-
projective,
if for all subspaces
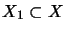 ,
,
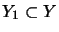 the map
the map
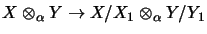 is a complete quotient map;
is a complete quotient map;
-
self dual,
if the algebraic embedding
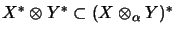 has a completely isometric extension
has a completely isometric extension
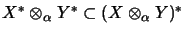 .
.
In many applications one finds the
Haagerup -tensor product.
It is not symmetric, but associative, injective,
projective and self dual.
Footnotes
- ...
30
- i.e., let
![$ [S_{ij}] \in M_p(\mathit{CB}(X_1,X_2)) $](img649.png) ,
,
![$ [T_{kl}] \in M_q(\mathit{CB}(Y_1,Y_2)) $](img650.png) ,
,
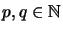 ,
then the norm of the linear operator
is estimated by
,
then the norm of the linear operator
is estimated by
![$\displaystyle \Vert [S_{ij} \otimes T_{kl}] \Vert _\mathrm{cb}
\leq
\Vert [S_{ij}] \Vert _\mathrm{cb}\Vert [T_{kl}] \Vert _\mathrm{cb}$](img652.png)
.

Remark: This is indeed an equality.
- ...itemnr:ORTPaxiom4.31
- (2)
 (3),(4):
Condition
(3),(4):
Condition
![[*]](crossref.png) is a special case of
is a special case of
![[*]](crossref.png) .
Let
.
Let
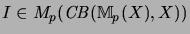 ,
,
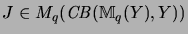 be matrices, which are algebraically the the identical mappings
of the vector spaces
be matrices, which are algebraically the the identical mappings
of the vector spaces
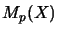 respectivly
respectivly
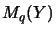 .
By assumption
.
By assumption
![[*]](crossref.png) we have
we have
Now
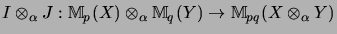 is the shuffle-map in
is the shuffle-map in
![[*]](crossref.png) .
.
(3),(4)
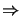 (2):
Let
(2):
Let
![$ [S_{ij}] \in M_p(\mathit{CB}(X_1,X_2)) $](img649.png) ,
,
![$ [T_{kl}] \in M_q(\mathit{CB}(Y_1,Y_2)) $](img650.png) ,
,
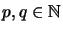 ,
and
,
and
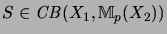 ,
,
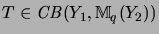 the corresponding operators.
By
the corresponding operators.
By
![[*]](crossref.png) holds
holds
We apply the shuffle map
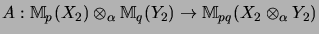 and obtain from
and obtain from
![[*]](crossref.png)
Hence
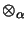 is jointly completely bounded.
is jointly completely bounded.
Subsections





Next: cross norms
Up: Tensor Products
Previous: Tensor Products
Contents
Index
Prof. Gerd Wittstock
2001-01-07
![[*]](crossref.png) and
and
![[*]](crossref.png) [BP91, Def. 5.9].
hold.
[BP91, Def. 5.9].
hold.
![]() is defined for each pair
is defined for each pair
![]() of operator spaces and endows
their algebraic tensor product
of operator spaces and endows
their algebraic tensor product
![]() with the structure of an
matrix normed space
with the structure of an
matrix normed space
![]() thuch that the following two properties
thuch that the following two properties
![[*]](crossref.png) and
and
![[*]](crossref.png) [BP91, Def. 5.9].
hold.
[BP91, Def. 5.9].
hold.
![]() -operator space tensor product
of
-operator space tensor product
of
![]() and
and
![]() and is denoted by
and is denoted by
![]() .
.
![[*]](crossref.png) may be replaced by the assumptions
may be replaced by the assumptions
![[*]](crossref.png) and
and
![[*]](crossref.png) .31
.31
![[*]](crossref.png) is equivalent to the following two
conditions: The
shuffle mappings
is equivalent to the following two
conditions: The
shuffle mappings
![[*]](crossref.png) is a special case of
is a special case of
![[*]](crossref.png) .
Let
.
Let
![[*]](crossref.png) we have
we have
![[*]](crossref.png) .
.
![]() (2):
Let
(2):
Let
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() ,
,
![]() the corresponding operators.
By
the corresponding operators.
By
![[*]](crossref.png) holds
holds
![[*]](crossref.png)