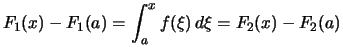 für
für ![[*]](crossref.png) )
)
![[*]](crossref.png) zum Mittelwertsatz).
zum Mittelwertsatz).
Bemerkung. Die folgenden Fakten ergeben zusammengenommen den Hauptsatz der Differential- und Integralrechnung:
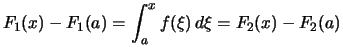 für
für ![[*]](crossref.png) )
)
![[*]](crossref.png) zum Mittelwertsatz).
zum Mittelwertsatz).
Es seien ![]() ein nicht entartetes Intervall
und
ein nicht entartetes Intervall
und
![]() stetig im Inneren von
stetig im Inneren von ![]() .
.
Für eine Funktion
![]() sind äquivalent:
sind äquivalent:
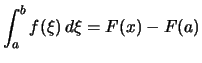 für alle
für alle
Bemerkung.
Dies ist ein erster Schritt zu Lösung von Differentialgleichungen. Umgekehrt nennt man Lösungen von Differentialgleichungen machmal auch Integrale.
Beweis (Hauptsatz der Diff.- u. Int.-Rechnung).
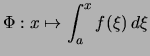 für
für ![[*]](crossref.png) ist
ist
![[*]](crossref.png) dort differenzierbar mit Ableitung
dort differenzierbar mit Ableitung ![[*]](crossref.png) ist
ist ![[*]](crossref.png) .
.
Bemerkung. Man kann den Hauptsatz der Differential- und Integral-Rechnung auf Regelfunktionen erweitern, wenn man die Differenzierbarkeit in allen Punkten etwas abschwächt: (vgl. Koenigsberger Kap. 9.10 und 11.4)
Hauptsatz der Diff.-u. Integralr. für Regelfunktionen.
Es sei ![]() ein nichtausgeartetes Intervall.
Für
ein nichtausgeartetes Intervall.
Für
![]() und
und
![]() sind äquivalent:
sind äquivalent:
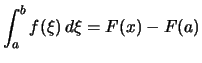 für alle
für alle
Bemerkung.
Aus dem Hauptsatz der Differential- und Integral-Rechnung
![[*]](crossref.png) und der Kettenregel
und der Kettenregel ![[*]](crossref.png) ergibt sich unmittelbar die
Substitutionsregel:
ergibt sich unmittelbar die
Substitutionsregel:
Es seien ![]() und
und ![]() Intervalle. Die Funktionen
Intervalle. Die Funktionen
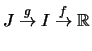
Wenn ![]() eine Stammfunktion von
eine Stammfunktion von ![]() ist, dann ist
ist, dann ist
![]() eine Stammfunktion zu
eine Stammfunktion zu
![]() .
.
D.h. für alle ![]() ,
, ![]() gilt
gilt
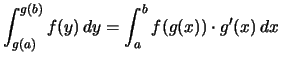
Bemerkung. Für die Anwendungen beachte man die Integralgrenzen der beiden Integral!