ehem. Hahn

Room: 428
Phone: +49681/302-3227
Email: This email address is being protected from spambots. You need JavaScript enabled to view it.
Research Interests:
- osculating cones to Brill-Noether loci,
- local structure of the moduli space of vector bundles,
- experimental methods of computer algebra in algebraic geometry,
- (relative) canonical resolutions of curves,
- K3 surfaces and Fano manifolds.
Teaching:
- Tutor: Mathematik für Informatiker 1, Winter 2020/21 (PD Apushkinskaya)
- Teaching Assistant: Mathematik für InformatikerInnen 2, Summer 2020 (Prof. Schreyer)
- Teaching Assistant: Mathematik für Informatiker 1, Winter 2019/20 (Prof. Schreyer)
- Lecturer: Seminar zur Algebraischen Topologie, Summer 2018
- Teaching Assistant : Mathematik für Naturwissenschaftler 1, Winter 2017/18 (Prof. Schulze-Pillot)
- Lecturer: Proseminar - Maple als Visualisierungswerkzeug, Winter 2017/18
- Teaching Assistant: Seminar über Riemannsche Flächen, Winter 2016/17 (Prof. Schreyer)
- Teaching Assistant: Mathematik für Informatiker 2, Summer 2016 (Dr. Michael Sagraloff)
- Teaching Assistant: Lineare Algebra 1, Winter 2015/16 (Prof. Johannes Rau)
- Teaching Assistant: Mathematik für Informatiker 2, Summer 2014
- Teaching Assistant: Mathematik für Informatiker 1, Winter 2013/14
- Teaching Assistant: Algebraische Flächen, Summer 2013
- H. Nyugen, M.Hoff, T. Hoang, On cylindrical smooth rational Fano fourfolds, available at https://arxiv.org/pdf/2101.04441.pdf
- M. Fortuna, M. Hoff, G. Mezzedimi, Unirational moduli spaces of some elliptic K3 surfaces, available at https://arxiv.org/pdf/2008.12077.pdf
- C. Bopp, M. Hoff, Moduli of lattice polarized K3 surfaces via relative canonical resolutions, available at https://arxiv.org/pdf/1704.02753.pdf
Papers:
- C. Bopp, M. Hoff, The relative canonical resolution: Macaulay2-package, experiments and conjectures, Journal of Software for Algebra and Geometry, Vol. 11 (2021), 15–24, DOI: 10.2140/jsag.2021.11.15
- M. Hoff, A. L. Knutsen, Brill-Noether general K3 surfaces with the maximal number of elliptic pencils of minimal degree, Geometriae Dedicata, electronically published on September 04, 2020, DOI: 10.1007/s10711-020-00565-z (to appear in print)
- G. H. Hitching, M. Hoff, P. E. Newstead, Nonemptiness and smoothness of twisted Brill-Noether loci, Annali di Matematica Pura ed Applicata, electronically published on June 26, 2020, DOI: 10.1007/s10231-020-01009-x (to appear in print)
- M. Hoff, G. Staglianò, New examples of rational Gushel-Mukai fourfolds, Mathematische Zeitschrift, 296,1585–1591(2020), DOI: 10.1007/s00209-020-02498-5
- M. Hoff, Focal schemes to families of secant spaces to canonical curves, Algorithmic and experimental methods in algebra, geometry, and number theory, 387-401 (2018). DOI: 10.1007/978-3-319-70566-8
- G. H. Hitching, M. Hoff, Tangent cones to generalised theta divisors and generic injectivity of the theta map. Compositio Mathematica, 153(12), 2643-2657 (2017). DOI:10.1112/S0010437X17007539
- C. Bopp, M. Hoff, Resolutions of general canonical curves on rational normal scrolls, Archiv der Mathematik (Basel) 105 (2015), no. 3, 239-249, DOI: 10.1007/s00013-015-0794-x
- M. Hoff, U. Mayer, The osculating cone to special Brill-Noether loci, Collectanea Mathematica 66 (2015), no. 3, 387-403,
DOI: 10.1007/s13348-015-0146-y - M. Hoff, Osculating cones to Brill–Noether loci for line and vector bundles on curves and relative canonical resolutions of curves, Ph.D. thesis (2017)
Pictures and Animations:
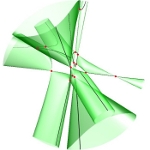
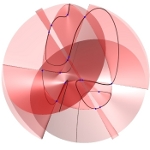
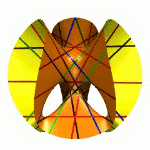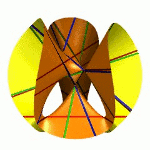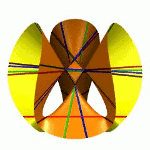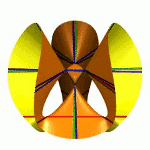
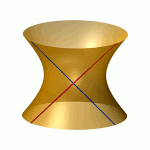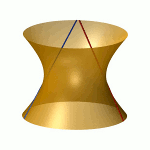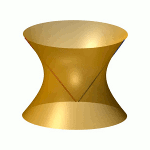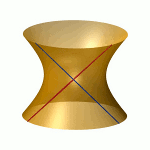
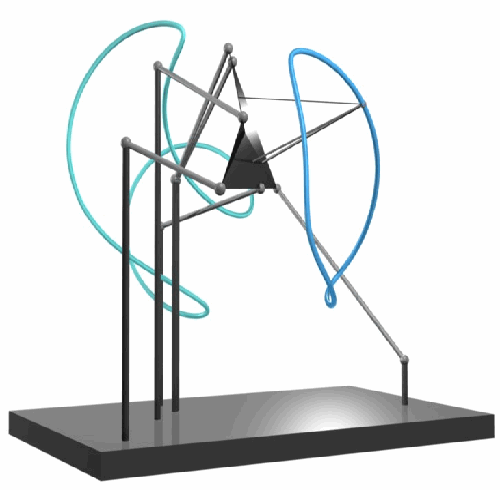
| To a general tetragonal canonical curve C of genus 6, we can associate a trigonal curve as follows. There is a pencil of planes intersecting C in the given g^1_4. Four different points in a plane has six connection lines which intersect in three further points. These further intersection points sweep out a trigonal curve C'. The union of C and C' is the osculating cone to the Brill-Noether locus W^0_4(C) at the given point g^1_4 of W^1_4(C). We denote by S the surface consisting of the connection lines swept out by the pencil of planes. Here you can see a real picture of the surface S with a highlighted plane. |  |
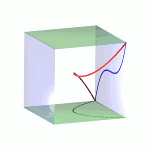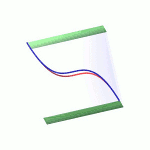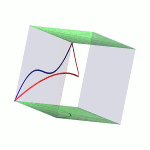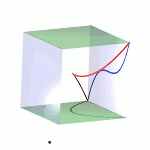
An animation of the surface S and a moving plane can be found here. The animation based on an example in "The osculating cone to special Brill-Noether loci".
Macaulay2-files:
| RelativeCanonicalResolution.m2 | Documentation | Computation of relative canonical resolution and Eagon-Northcott type complexes |
| ExtensionsAndTorsWithLimitedDegree.m2 | Documentation | Computation of the homogeneous components of the graded modules Ext^i(M,N) and Tor^i(M,N) with a fixed degree limit |
| M2codeThesisHoff.m2 / constructionOfTheOsculatingCone.m2 | M2 code for my thesis | |
| relativeCanonicalResolutionsAndK3Surfaces.m2 | ancillary file to "Moduli of lattice polarized K3 surfaces via relative canonical resolutions" | |
| surface.m2, surface-char0.m2 | ancillary files to "New examples of rational Gushel-Mukai fourfolds" | |
| ancillary file to "Brill-Noether general K3 surfaces with the maximal number of elliptic pencils of minimal degree" | ||
| ConstructingEllipticK3Surfaces-supportingM2files.zip | ancillary files to "Unirational moduli spaces of some elliptic K3 surfaces" |
Experiments concerning relative canonical resolutions:
The webpage (click here) lists all experimental results concerning the shape of relative canonical resolutions done with the Macaulay2-package "RelativeCanonicalResolution.m2"
Education:
- 03/2017 - present: Postdoc at the Universität des Saarlandes
- 09/2012 - 03/2017: Ph.D. student at the Universität des Saarlandes
- 09/2012 - 03/2013: DAAD study visit at the University of Oslo, Norway
- 04/2012 - 08/2012: M. Sc. in Mathematics at the Universität des Saarlandes
- 04/2008 - 03/2012: B. Sc. in Mathematics at the Universität des Saarlandes