




Next: Der Spalten-Hilbertraum
Up: Hilbertsche Operatorräume
Previous: Die Räume
Der Raum
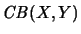 der vollständig beschränkten Abbildungen
zwischen
zwei homogenen hilbertschen Operatorräumen X,Y hat die folgenden
Eigenschaften (vgl. [MP95, Prop. 1.2]):
der vollständig beschränkten Abbildungen
zwischen
zwei homogenen hilbertschen Operatorräumen X,Y hat die folgenden
Eigenschaften (vgl. [MP95, Prop. 1.2]):
- 1.
-
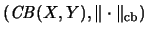 ist ein Banachraum.
ist ein Banachraum.
- 2.
-
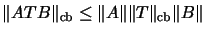 für alle A,
für alle A,
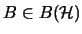 ,
,
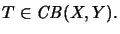
- 3.
-
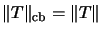 für alle T mit
für alle T mit
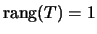 .
.
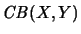 ist damit ein
symmetrisch normiertes Ideal (s.n. Ideal) im Sinne von
Calkin, Schatten [Sch70] und Gohberg [GK69].
Standardbeispiele für s.n. Ideale sind
die bekannten
Schattenideale:
ist damit ein
symmetrisch normiertes Ideal (s.n. Ideal) im Sinne von
Calkin, Schatten [Sch70] und Gohberg [GK69].
Standardbeispiele für s.n. Ideale sind
die bekannten
Schattenideale:
Viele, aber nicht alle, s.n. Ideale können als vollständig
beschränkte Abbildungen zwischen homogenen, hilbertschen Operatorräumen
realisiert werden. Wie so oft ist am meisten bekannt über Schattenideale.
Das erste Ergebnis in dieser Richtung war
isometrisch [ER91, Cor. 4.5]. Wir haben isometrisch bzw. isomorph (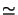 )
[Mat94], [MP95], [Lam97]:
Einzig ist darin
)
[Mat94], [MP95], [Lam97]:
Einzig ist darin
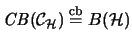 eine vollständig isometrische
Isomorphie (vgl. [Ble95, Thm. 3.4]).
Von besonderem Interesse ist
eine vollständig isometrische
Isomorphie (vgl. [Ble95, Thm. 3.4]).
Von besonderem Interesse ist
Hier haben wir eine neue natürliche Norm auf den
nuklearen Operatoren,
die nicht gleich der kanonischen ist.
Auch im endlichdimensionalen Fall ist nur
bekannt [Pau92, Thm. 2.16]. Das Bestimmen des exakten Wertes ist ein noch offenes
Problem;
Paulsen vermutet, daß die obere Schranke angenommen wird [Pau92, p. 121].
Seien E ein Banachraum und
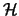 ein Hilbertraum. Dann ist ein Operator
ein Hilbertraum. Dann ist ein Operator
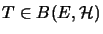 genau dann vollständig beschränkt
von
genau dann vollständig beschränkt
von
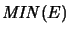 nach
nach
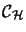 , wenn er
absolut-2-summierend
[Pie67] von
E nach
, wenn er
absolut-2-summierend
[Pie67] von
E nach
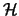 ist (vgl. [ER91, Thm. 5.7]):
ist (vgl. [ER91, Thm. 5.7]):
mit
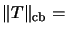
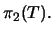





Next: Der Spalten-Hilbertraum
Up: Hilbertsche Operatorräume
Previous: Die Räume
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04
![]() ein Hilbertraum. Dann ist ein Operator
ein Hilbertraum. Dann ist ein Operator
![]() genau dann vollständig beschränkt
von
genau dann vollständig beschränkt
von
![]() nach
nach
![]() , wenn er
absolut-2-summierend
[Pie67] von
E nach
, wenn er
absolut-2-summierend
[Pie67] von
E nach
![]() ist (vgl. [ER91, Thm. 5.7]):
ist (vgl. [ER91, Thm. 5.7]):