Next: Über dieses Dokument ...
Up: Was sind Operatorräume ?
Previous: Literatur
- Unterindex
-
-
- see Abbildung
-
- see Abbildungsraum
-
- see Amplifikation
-
- see Axiome
-
- see Beispiele
-
- see bilineare Abbildung
-
- see C*-Algebra
-
- see Haagerup-Tensorprodukt
-
- see hilbertscher Op.-raum
-
- see injektives Op.-Tensorprodukt
-
- see Lemma von
-
- see Modulhomomorphismus
-
- see multilineare Abbildung
-
- see Operatoralgebra
-
- see Operatormodul
-
- see Operatorraum
-
- see Operatorraum-Tensorprodukt
-
- see projektives Op.-Tensorprodukt
-
- see Satz von
-
- see spezielle Operatorräume
-
- see vollständig beschränkte Abbildung
- Abbildung
- absolut-2-summierende
- Die Abbildungen
- Hilbert-Schmidt-
- Die Abbildungen
- integrale
- Vollständig integrale Abbildungen
- nukleare
- Die Abbildungen
| Vollständig nukleare Abbildungen
- shuffle-
- see Operatorraum-Tensorprodukt
| Operatorraum-Tensorprodukte
- vollständig beschränkte
- Geschichte
| see vollständig beschränkte Abbildung
- vollständig integrale
- Vollständig integrale Abbildungen
- Charakterisierung
- Vollständig integrale Abbildungen
- vollständig nukleare
- Vollständig nukleare Abbildungen
- Charakterisierung
- Vollständig nukleare Abbildungen
- vollständig positive
- Geschichte
- vollständige Quotienten-
- Der adjungierte Operator
- zwischen homogenen hilbertschen Operatorräumen
- see hilbertscher Operatorraum
- Abbildungsraum
|
- vollständig integrale Abbildungen
- Vollständig integrale Abbildungen
- vollständig nukleare Abbildungen
- Vollständig nukleare Abbildungen
- absolut matrixkonvex
- Matrixkonvexität
- abstrakter Operatorraum
- see Operatorraum
- Ähnlichkeitsproblem
- Vollständig beschränkte multilineare Abbildungen
- Algebrenhomomorphismus
- Operatoralgebren
- allgemein(e)
- Amplifikation
- see bilineare Abbildung
- Amplifikation
- Grundbegriffe
|
- allgemeine
- see bilineare Abbildung
- bilineare Abbildung
- see bilineare Abbildung
- äußeres Tensorprodukt
- Das äußere Tensorprodukt von Hilbert-C*-Moduln
- automatische vollständige Beschränktheit
- Vollständig beschränkte multilineare Abbildungen
- Axiome
- von Ruan
- Operatormodul
- Operatormoduln über C*-Algebren
- Operatorraum
- Grundbegriffe
- Beispiele
- Beispiele
|
- Haagerup-Tensorprodukt
- Formeln für das Haagerup-Tensorprodukt
- hilbertsche Operatorräume
- Die Räume
- injektives Op.-Tensorprodukt
- Formeln für das injektive
- Modul-Haagerup-Tensorprodukt
- Beispiele
- Operatoralgebra
- Operatoralgebren
| Beispiele
- Operatormodul
- Beispiele für Operatormoduln
- Operatorraum
- Grundbegriffe
| Matrizen über einem Operatorraum
- vollständig lokal reflexiver
- Beipiele
- projektives Op.-Tensorprodukt
- Formeln für das projektive
- strukturelles Element
- Matrixextremalpunkte
- bilineare Abbildung
- allgemein vollständig beschränkte
- see projektives Operatorraum-Tensorprodukt
|
| Allgemein vollständige Beschränktheit
- jointly completely bounded
- Vollständig beschränkte bilineare Abbildungen
- Norm
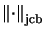
- Allgemein vollständige Beschränktheit
- Raum
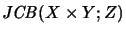
- Allgemein vollständige Beschränktheit
- Transposition
- Allgemein vollständige Beschränktheit
- allgemeine Amplifikation
|
-
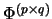
- Amplifikation
- Matrixdualität
- Amplifikation
- Operatoralgebren
|
|
- auf quadratischen Matrizen
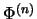
- Amplifikation
- auf Rechteckmatrizen
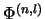
- Amplifikation
- Bilinearform
- automatisch vollständig beschränkte
- Vollständig beschränkte multilineare Abbildungen
- Linearisierung
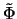
- Amplifikation
- transponierte Abbildung
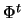
- Allgemein vollständige Beschränktheit
- transponierte Abbildung
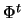
- Vollständige Beschränktheit
- vollständig beschränkte
- Operatoralgebren
| see Haagerup-Tensorprodukt
|
| Vollständige Beschränktheit
- nte Norm
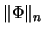
- Vollständige Beschränktheit
- Darstellung
- Darstellung
- Norm
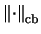
- Vollständige Beschränktheit
- Raum
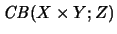
- Vollständige Beschränktheit
- Transposition
- Vollständige Beschränktheit
- Bipolarensatz
- Bipolarensätze
- bridging maps
- Vollständig beschränkte multilineare Abbildungen
- Calkin-Algebra
- Vollständig beschränkte Modulhomomorphismen
-
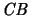 -Abbildungsraum
-Abbildungsraum
- Abbildungsräume
-
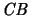 -Idealeigenschaft
-Idealeigenschaft
- Faktorisierung durch den Spalten-Hilbertraum
| Abbildungsräume
- Charakterisierung
- vollständig lokal reflexiver Operatorräume
- Vollständige lokale Reflexivität
- Christensen
- Satz von
- Vollständig beschränkte multilineare Abbildungen
- C*-Algebra
- Grundbegriffe
| Multiplikative Strukturen
| Operatoralgebren
| Hilbert-C*-Moduln
| Beispiele
|
- injektive
- Vollständig beschränkte Modulhomomorphismen
- kommutative
- Grundbegriffe
| Konstruktion von
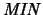 :
| Beipiele
| Vollständig beschränkte multilineare Abbildungen
:
| Beipiele
| Vollständig beschränkte multilineare Abbildungen
- nukleare
- Beipiele
- Darstellungssatz
- für vollständig beschränkte Modulhomomorphismen
- Vollständig beschränkte Modulhomomorphismen
- für vollständig beschränkte multilineare Abbildungen
- Vollständig beschränkte multilineare Abbildungen
- Operatormodul
- Operatormoduln über C*-Algebren
- Derivation
- innere
- Vollständig beschränkte multilineare Abbildungen
- vollständig beschränkte
- Vollständig beschränkte multilineare Abbildungen
- Derivationsproblem
- Vollständig beschränkte multilineare Abbildungen
- dominieren
- Grundbegriffe
| Beispiele
| Beispiele
- Dual
- eines Operatorraums
- see Operatorraum
- Operatorraum-Tensornorm
- see Operatorraum-Tensornorm
| Duales Operatorraum-Tensorprodukt
- Operatorraum-Tensorprodukt
- see Operatorraum-Tensorprodukt
| Duales Operatorraum-Tensorprodukt
- Einbettung
- kanonische
- Der Dual
| Vollständig integrale Abbildungen
- elementarer Operator
- Modulabbildungen zwischen Hilbert-C*-Moduln
- endlichrangige Abbildungen
- Abbildungsräume
- Faktorisierung
- durch den Spalten-Hilbertraum
- see hilbertscher Operatorraum
- Fortsetzungssatz
- für vollständig beschränkte Modulhomomorphismen
- Vollständig beschränkte Modulhomomorphismen
- für vollständig beschränkte multilineare Abbildungen
- Vollständig beschränkte multilineare Abbildungen
- Grothendieck
- -Konstante KG
- Vollständig beschränkte multilineare Abbildungen
- H-Tensorprodukt
- Haagerup-Tensorprodukt
- Grundstufe
- see Operatorraum
- H-Tensorprodukt
- Haagerup-Tensorprodukt
- Haagerup-Tensor-
- norm
- Infimum-Formel
- Haagerup-Tensorprodukt
- Minimum-Formel
- Formeln für das Haagerup-Tensorprodukt
- Summen-Formel
- Formeln für das Haagerup-Tensorprodukt
- Supremum-Formel
- Formeln für das Haagerup-Tensorprodukt
- produkt
- H-Tensorprodukt
- Haagerup-Tensorprodukt
-
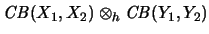
- Formeln für das Haagerup-Tensorprodukt
- Interpolation
- Haagerup-Tensorprodukt
- Lemma von Blecher und Paulsen
- Formeln für das Haagerup-Tensorprodukt
- mit Spalten-Hilbertraum
- Formeln für das Haagerup-Tensorprodukt
| Formeln für das Haagerup-Tensorprodukt
- mit Zeilen-Hilbertraum
- Formeln für das Haagerup-Tensorprodukt
| Formeln für das Haagerup-Tensorprodukt
- shuffle-Abbildung
- Formeln für das Haagerup-Tensorprodukt
| Formeln für das Haagerup-Tensorprodukt
- tensorielles Matrixprodukt
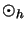
- Formeln für das Haagerup-Tensorprodukt
- Hilbert-C*-Modul
- Rechte und linke Hilbert-C*-Moduln
- konjugierter
- Konjugierter Hilbert-C*-Modul
- hilbertscher Operatorraum
- Abbildungen
- Die Abbildungen
- homogener
- Die Räume
- vollständig selbstdualer
- Die Räume
- maximaler
- Die Räume
- minimaler
- Die Räume
- Operatorhilbertraum
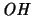
- Interpolation
- Operatorhilbertraum
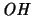
- Die Räume
- Operatorhilbertraum
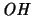
- als Operatoralgebra
- Beispiele
- Spalten-Hilbertraum
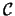
- Beispiele
- Spalten-Hilbertraum
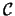
- Beispiele
- Spalten-Hilbertraum
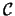
- Beispiele für konjugierte Hilbert-C*-Moduln
- Spalten-Hilbertraum
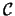
- Die Räume
- Spalten-Hilbertraum
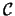
- Der Spalten-Hilbertraum
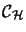
- Spalten-Hilbertraum
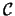
- Charakterisierungen
- Charakterisierungen
- Spalten-Hilbertraum
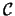
- Faktorisierung durch den
- Faktorisierung durch den Spalten-Hilbertraum
- Spalten-Hilbertraum
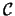
- als Operatoralgebra
- Beispiele
- Zeilen-Hilbertraum
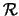
- Beispiele
- Zeilen-Hilbertraum
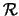
- Beispiele
- Zeilen-Hilbertraum
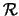
- Beispiele für konjugierte Hilbert-C*-Moduln
- Zeilen-Hilbertraum
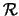
- Die Räume
- Zeilen-Hilbertraum
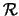
- als Operatoralgebra
- Beispiele
- Hochschild-Kohomologie
- Vollständig beschränkte multilineare Abbildungen
- Homomorphismus
- Vollständig beschränkte Modulhomomorphismen
- ICM 1986
- Geschichte
- Ideal
- einer Operatoralgebra
- see Operatoralgebra
- Schatten-Klasse
- Die Abbildungen
- symmetrisch normiertes
- Die Abbildungen
- Idealeigenschaft
- Abbildungsräume
- injektive(s) Operatorraum-
- Tensornorm
- Tensorprodukt
-
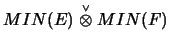
- Formeln für das injektive
- und
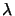 -Tensorprodukt
-Tensorprodukt
- Formeln für das injektive
- inneres Tensorprodukt
- Das innere Tensorprodukt von Hilbert-C*-Moduln
- Interpolation von Operatorräumen
- Interpolation
- Interpolationsraum
- Interpolation
- jointly completely bounded
- see bilineare Abbildung!allgemein vollständig beschränkte
- Kommutant
- Vollständig beschränkte Modulhomomorphismen
- konjugierter Hilbert-C*-Modul
- Konjugierter Hilbert-C*-Modul
- konkreter Operatorraum
- see Operatorraum
- Konvexkombination
- Matrix-
- Matrixkonvexität
- Matrixabsolut-
- Matrixkonvexität
- Kreuznorm
- Kreuznormen
- Lemma von
| see Satz von
- Blecher und Paulsen
- Formeln für das Haagerup-Tensorprodukt
- Smith
- Lemma von Smith
- lokal reflexiv
- Vollständige lokale Reflexivität
- vollständig
- Vollständige lokale Reflexivität
- M-Ideal
- Vollständige lokale Reflexivität
- Mapping space
- see Abbildungsraum
- Matrixabsolutkonvexkombination
- Matrixkonvexität
- Matrixdualität
- see bilineare Abbildung
- Matrixkegel
- Matrixkonvexität
- matrixkonvex
- Matrixkonvexität
- absolut
- Matrixkonvexität
- Matrixkonvexkombination
- Matrixkonvexität
- matrixnormierter Raum
- see Raum
- Matrixpolare
- Bipolarensätze
- absolute
- Bipolarensätze
- Matrizen
- Menge von
- Matrixkonvexität
- Matrizenmultiplikation
- Operatoralgebren
- Menge von Matrizen
- Matrixkonvexität
- Modulhomomorphismus
- (A1,A2)-
- Vollständig beschränkte Modulhomomorphismen
- A-Bi-
- Vollständig beschränkte Modulhomomorphismen
- Bi-
- Vollständig beschränkte Modulhomomorphismen
- normaler
- Vollständig beschränkte Modulhomomorphismen
- selbstadjungierter
- Vollständig beschränkte Modulhomomorphismen
- singulärer
- Vollständig beschränkte Modulhomomorphismen
- vollständig beschränkter
- Vollständig beschränkte Modulhomomorphismen
- Darstellung
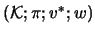
- Vollständig beschränkte Modulhomomorphismen
- Darstellungssatz
- Vollständig beschränkte Modulhomomorphismen
- Fortsetzungssatz
- Vollständig beschränkte Modulhomomorphismen
- Modul-Haagerup-Tensorprodukt
- Vollständig beschränkte Modulhomomorphismen
| Beispiele
- Zerlegungssatz
- Vollständig beschränkte Modulhomomorphismen
- multilineare Abbildung
- Amplifikation
- Vollständig beschränkte multilineare Abbildungen
- Linearisierung
- Vollständig beschränkte multilineare Abbildungen
- Haagerup-Tensorprodukt
- Vollständig beschränkte multilineare Abbildungen
- symmetrische
- Vollständig beschränkte multilineare Abbildungen
- vollständig beschränkte
- Vollständig beschränkte multilineare Abbildungen
- Darstellungssatz
- Vollständig beschränkte multilineare Abbildungen
- Fortsetzungssatz
- Vollständig beschränkte multilineare Abbildungen
- vollständig beschränkte symmetrische
- Zerlegungssatz
- Vollständig beschränkte multilineare Abbildungen
- vollständig positive
- Vollständig beschränkte multilineare Abbildungen
- normal
- Modulhomomorphismus
- see Modulhomomorphismus
- Operator
- adjungierter
- Der adjungierte Operator
- von Hilbert-C*-Moduln
- Modulabbildungen zwischen Hilbert-C*-Moduln
- elementarer
- Modulabbildungen zwischen Hilbert-C*-Moduln
- Operatoralgebra
- abstrakte
- Operatoralgebren
- Ideal einer
- Operatoralgebren
- konkrete
- Operatoralgebren
- Satz von Ruan
- Operatoralgebren
- Operatorideal
- Abbildungsräume
- Operatormodul
- see Modulhomomorphismus
|
- (A1,A2)-
- Operatormoduln über C*-Algebren
- abstrakter
- Operatormoduln über C*-Algebren
- Beispiele
- Beispiele für Operatormoduln
- Darstellungssatz
- Operatormoduln über C*-Algebren
- konkreter
- Operatormoduln über C*-Algebren
- Operatorbimodul
- A-
- Operatormoduln über C*-Algebren
- Operatorraum
- Geschichte
| Grundbegriffe
|
- abstrakter
- Satz von Ruan
- Dual
- Der Dual
- endlichdimensionaler
- Vollständige lokale Reflexivität
- Grundstufe
- Grundbegriffe
- hilbertscher
- Die Räume
| see hilbertscher Operatorraum
- homogener
- Grundbegriffe
- vollständig selbstdualer
- see hilbertscher Operatorraum
- injektiver
- Der Spalten-Hilbertraum
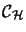
- interpolierter
- Interpolation
- kanonischer, eines Hilbert-C*-Moduls
- Die kanonische Operatorraumstruktur
- konkreter
- Grundbegriffe
| Satz von Ruan
- Matrizenstufe
- Grundbegriffe
| Matrizen über einem Operatorraum
- maximaler
-
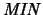 und
und
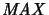 | Bipolarensätze
| Bipolarensätze
- minimaler
-
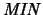 und
und
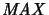 | Bipolarensätze
| Bipolarensätze
- Operatorraumnorm
- Grundbegriffe
- Quotient
- Unterräume und Quotienten
- reflexiv
- Einige Formeln
- Unterraum
- Unterräume und Quotienten
- vollständig lokal reflexiver
- Vollständige lokale Reflexivität
- Operatorraum-Tensor-
- norm
- duale
- Haagerup-
- see Haagerup-Tensornorm
- injektive
- see injektive
- maximale
- see projektive
- minimale
- see injektive
- projektive
- see projektive
- räumliche
- see injektive
- produkt
- Assoziativität
- Operatorraum-Tensorprodukte
- Axiome
- Operatorraum-Tensorprodukte
- duales
- Haagerup-
- see Haagerup-Tensorprodukt
- injektives
- see injektives
- Injektivität
- Operatorraum-Tensorprodukte
- Kreuznorm
- Kreuznormen
- maximales
- see projektives
- minimales
- see injektives
- projektives
- see projektives
- Projektivität
- Operatorraum-Tensorprodukte
- räumliches
- see injektives
- Selbstdualität
- Operatorraum-Tensorprodukte
- shuffle-Abbildung
- Symmetrie
- Operatorraum-Tensorprodukte
- Operatorraumschnitt
- Schnitt und Summe
- Operatorraumsumme
- Schnitt und Summe
- Operatorraumtensornorm
- projektive
- Vollständig nukleare Abbildungen
- Operatorsysteme
- Geschichte
- Paulsen
- Vermutung von
- Die Abbildungen
- projektive(s) Operatorraum-
- Tensornorm
- Tensorprodukt
-
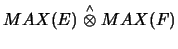
- Formeln für das projektive
- Fourier-Algebra
- Formeln für das projektive
- Prädual einer von Neumann-Algebra
- Formeln für das projektive
- Spalten-Hilbertraum
- Formeln für das projektive
- und
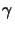 -Tensorprodukt
-Tensorprodukt
- Formeln für das projektive
- Zeilen-Hilbertraum
- Formeln für das projektive
- Quotient
- eines Operatorraums
- see Operatorraum
- Quotientenabbildung
- vollständige
- see Abbildung
- Raum
- matrixnormierter
- Grundbegriffe
- Ruan
- Axiome
- Operatormodul
- Operatormoduln über C*-Algebren
- Operatorraum
- Grundbegriffe
- Satz von
- Satz von Ruan
- Satz
- Bipolaren-
- Bipolarensätze
- Trennungs-
- Trennungssätze
- Satz von
| see Lemma von
- Christensen
- Vollständig beschränkte multilineare Abbildungen
- Ruan
- Satz von Ruan
- für Operatoralgebren
- Operatoralgebren
- Schattenideal Sp
- Die Abbildungen
- Schattenideale Sp
- Beispiele
- Operatorraumstruktur der
- Interpolation
- Schnitt von Operatorräumen
- Schnitt und Summe
- Schur-Produkt
- Beispiele
- selbstadjungiert
- Algebra in
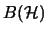
- Operatoralgebren
- shuffle-Abbildung
- see Operatorraum-Tensorprodukt
| Operatorraum-Tensorprodukte
- singulär
- Modulhomomorphismus
- see Modulhomomorphismus
- Spalten-Hilbertraum
- see hilbertscher Operatorraum
- Spaltennorm
- Charakterisierungen
- Spaltenraum
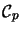
- Spalten und Zeilen eines
- spezielle Operatorräume
-
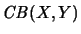
- Der Raum
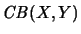
- maximaler hilbertscher Operatorraum
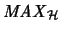
- Die Räume
- minimaler hilbertscher Operatorraum
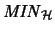
- Die Räume
- Operatorhilbertraum
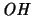
- Interpolation
- Operatorhilbertraum
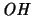
- Die Räume
- Operatorraumschnitt
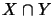
- Schnitt und Summe
- Operatorraumsumme X+Y
- Schnitt und Summe
- Spalten-Hilbertraum
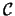
- Die Räume
- Zeilen-Hilbertraum
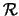
- Die Räume
- Standarddual
- Der Dual
- *-Darstellung
- Vollständig beschränkte Modulhomomorphismen
- *-Homomorphismus
- Vollständig beschränkte Modulhomomorphismen
- strukturelles Element
- Matrixextremalpunkte
- Summe von Operatorräumen
- Schnitt und Summe
- symmetrisch
- multilineare Abbildung
- Vollständig beschränkte multilineare Abbildungen
- Tensornorm
- von Operatorräumen
- see Operatorraum-Tensornorm
- Tensorprodukt
- äußeres
- von Hilbert-C*-Moduln
- Das äußere Tensorprodukt von Hilbert-C*-Moduln
- inneres
- von Hilbert-C*-Moduln
- Das innere Tensorprodukt von Hilbert-C*-Moduln
- von Operatorräumen
- see Operatorraum-Tensorprodukt
- Haagerup-
- see Haagerup-
- Kreuznorm
- Kreuznormen
- Topologie
- nichtkommutative
- Geschichte
- Trennungssatz
- Trennungssätze
- Unterraum
- eines Operatorraums
- see Operatorraum
- vollständig beschränkt
- automatisch
- Vollständig beschränkte multilineare Abbildungen
- Modulhomomorphismus
- Vollständig beschränkte Modulhomomorphismen
- vollständig beschränkte Abbildung
- Grundbegriffe
|
|
- vollständig isometrisch
- Grundbegriffe
- vollständig kontrahierend
- Grundbegriffe
- vollständige Quotientenabbildung
- Grundbegriffe
- vollständig isometrisch
- see vollständig beschränkte Abbildung
| Der adjungierte Operator
- vollständig kontrahierend
- see vollständig beschränkte Abbildung
- vollständig lokal reflexiv
- Vollständige lokale Reflexivität
- vollständig positiv
- Vollständig beschränkte Modulhomomorphismen
- multilineare Abbildung
- Vollständig beschränkte multilineare Abbildungen
- vollständige Quotientenabbildung
- see vollständig beschränkte Abbildung
- Zeilen-Hilbertraum
- see hilbertscher Operatorraum
- Zeilennorm
- Charakterisierungen
- Zeilenraum
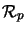
- Spalten und Zeilen eines
- Zerlegungssatz
- für selbstadjungierte vollständig beschränkte Bimodulhomomorphismen
- Vollständig beschränkte Modulhomomorphismen
- für vollständig beschränkte symmetrische multilineare Abbildungen
- Vollständig beschränkte multilineare Abbildungen
- von Tomiyama-Takesaki
- Vollständig beschränkte Modulhomomorphismen
- Zustandsraum
- verallgemeinerter
- Matrixextremalpunkte
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04
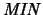 :
| Beipiele
| Vollständig beschränkte multilineare Abbildungen
:
| Beipiele
| Vollständig beschränkte multilineare Abbildungen
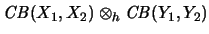
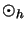
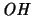
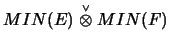
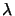 -Tensorprodukt
-Tensorprodukt
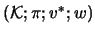
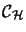
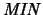 und
und
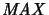 | Bipolarensätze
| Bipolarensätze
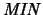 und
und
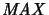 | Bipolarensätze
| Bipolarensätze
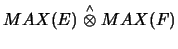
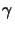 -Tensorprodukt
-Tensorprodukt