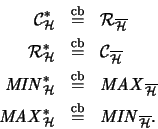Ein Operatorraum X heißt
hilbertsch,
wenn die Grundstufe M1(X) ein Hilbertraum
![]() ist.
Ein Operatorraum X heißt
homogen, wenn jeder beschränkte Operator
ist.
Ein Operatorraum X heißt
homogen, wenn jeder beschränkte Operator
![]() vollständig beschränkt ist und
vollständig beschränkt ist und
![]() [Pis96].
[Pis96].
Der minimale
![]() und der maximale
und der maximale
![]() hilbertsche Operatorraum, der
Spalten-Hilbertraum
hilbertsche Operatorraum, der
Spalten-Hilbertraum
![]() und
der
Zeilen-Hilbertraum
und
der
Zeilen-Hilbertraum
![]() sind homogene hilbertsche Operatoräume auf dem Hilbertraum
sind homogene hilbertsche Operatoräume auf dem Hilbertraum
![]() .
.
Darüberhinaus haben wir für zwei Hilberträume
![]() und
und
![]() vollständige isometrische Isomorphismen [ER91, Thm. 4.1]
[Ble92b, Prop. 2.2]
vollständige isometrische Isomorphismen [ER91, Thm. 4.1]
[Ble92b, Prop. 2.2]
Der Operatorraumschnitt und die Operatorraumsumme je zweier homogener hilbertscher Operatorräume sind wieder homogene hilbertsche Operatorräume [Pis96].
Die Operatorräume stehen in den folgenden
Dualitäten
[Ble92b, Prop. 2.2]
[Ble92a, Cor. 2.8]: