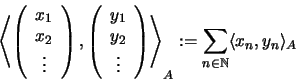Next: Der Zeilenraum
Up: Grundkonstruktionen
Previous: Grundkonstruktionen
Direkte Summe und Spaltenraum
Seien
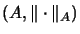 eine C*-Algebra und
Xi,
eine C*-Algebra und
Xi,
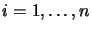 ,
rechte Hilbert-C*-Moduln
über A. Die Norm
,
rechte Hilbert-C*-Moduln
über A. Die Norm
macht aus der algebraisch direkten Summe der Xi einen rechten
Hilbert-C*-Modul über A. Die Modulabbildung wird durch
erklärt. Das innere Produkt definiert man durch:
Wenn gilt
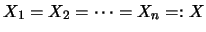 , so schreibt man für diesen Hilbert-C*-Modul
Cn(X).
Die Einbettung von Cn(X) in
, so schreibt man für diesen Hilbert-C*-Modul
Cn(X).
Die Einbettung von Cn(X) in
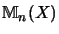 als erste Spalte ist eine
vollständige Isometrie.
als erste Spalte ist eine
vollständige Isometrie.
Für einen linken Hilbert-C*-Modul X bezeichne Cn(X)die Teilmenge von Mn(X), deren Elemente nur in der ersten Spalten Einträge
haben. Als Unterraum von Mn(X) ist Cn(X) ein linker Hilbert-C*-Modul
über Mn(A).
Seien Xn für
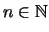 rechte
Hilbert-C*-Moduln über einer C*-Algebra
rechte
Hilbert-C*-Moduln über einer C*-Algebra
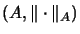 .
Die Menge
.
Die Menge
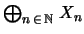 wird definiert durch
wird definiert durch
Mit
wird
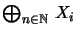 zu einem rechten Hilbert-C*-
Modul über A.
Wenn gilt
zu einem rechten Hilbert-C*-
Modul über A.
Wenn gilt
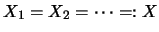 ,
so schreibt man für diesen
Hilbert-C*-Modul
,
so schreibt man für diesen
Hilbert-C*-Modul
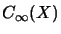 .
.
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04
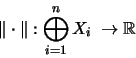
![]() rechte
Hilbert-C*-Moduln über einer C*-Algebra
rechte
Hilbert-C*-Moduln über einer C*-Algebra
![]() .
Die Menge
.
Die Menge
![]() wird definiert durch
wird definiert durch