




Next: The space
Up: Elementary constructions
Previous: Matrices over an operator
Contents
Index
The space 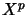 of
of 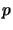 -tupels over an operator space
-tupels over an operator space  can be made into an operator
space for instance by reading the
can be made into an operator
space for instance by reading the 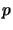 -tupels as
-tupels as 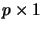 - or as
- or as
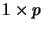 -matrices. This leads to the frequently used
columns and
rows of an operator space
-matrices. This leads to the frequently used
columns and
rows of an operator space  :
:
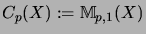
and
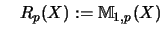
.
The first matrix level of these spaces are
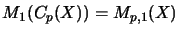
and
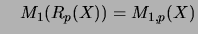
, respectively.
If
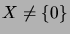 , the spaces
, the spaces 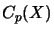 and
and 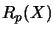 are not completely isometric. In
general even the first matrix levels
are not completely isometric. In
general even the first matrix levels
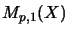 and
and
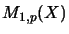 are not isometric.
are not isometric.
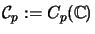 is called the
p-dimensional column space
and
is called the
p-dimensional column space
and
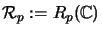 the
p-dimensional row space.
the
p-dimensional row space.
The first matrix levels of
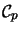 and
and
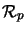 are isometric to
are isometric to 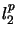 ,
but
,
but
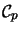 and
and
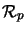 are not
completely isometric .
are not
completely isometric .
Prof. Gerd Wittstock
2001-01-07
![]() is called the
p-dimensional column space
and
is called the
p-dimensional column space
and
![]() the
p-dimensional row space.
the
p-dimensional row space.
![]() and
and
![]() are isometric to
are isometric to ![]() ,
but
,
but
![]() and
and
![]() are not
completely isometric .
are not
completely isometric .