



Next: Injective operator spaces
Up: and
Previous: Construction of :
Contents
Index
For a index set 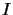 ,
,
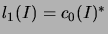 .
.
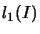 is an operator space as
dual of the commutative
is an operator space as
dual of the commutative 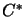 -algebra
-algebra 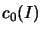 , and each bounded
linear mapping
, and each bounded
linear mapping
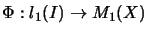 is automatically completely bounded with
is automatically completely bounded with
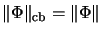 .17
.17
Each Banach space18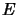 is isometric to a quotient of
is isometric to a quotient of
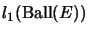 . Thus the operator space
. Thus the operator space
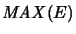 is given as a quotient of
is given as a quotient of
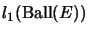 .
.
For
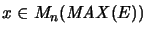 we have
we have
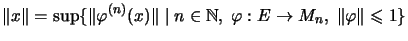
.
The unit ball of
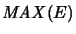 is given as the absolute matrix bipolar of
is given as the absolute matrix bipolar of
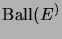 .
.
Footnotes
- ....17
- I. e.
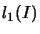 is a
is a
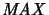 -space.
-space.
- ... space18
-
A similar construction is possible for normed spaces.
Prof. Gerd Wittstock
2001-01-07
![]() is isometric to a quotient of
is isometric to a quotient of
![]() . Thus the operator space
. Thus the operator space
![]() is given as a quotient of
is given as a quotient of
![]() .
.
![]() we have
we have