




Next: Completely nuclear mappings
Up: What are operator spaces?
Previous: -extreme points
Contents
Index
Let 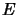 ,
, 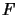 be Banach spaces.
We consider a linear subspace
be Banach spaces.
We consider a linear subspace 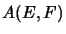 of the space
of the space 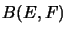 of the continuous operators between
of the continuous operators between 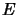 and
and
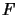 which contains all finite rank maps
and is a Banach space with respect to a given norm.
Furthermore, it is usually required that
which contains all finite rank maps
and is a Banach space with respect to a given norm.
Furthermore, it is usually required that 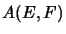 be defined for all pairs
of Banach spaces
be defined for all pairs
of Banach spaces 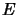 and
and 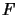 .
Such a space is called - according to A. Grothendieck - a
mapping space
.
.
Such a space is called - according to A. Grothendieck - a
mapping space
.
Analogously, we call an operator space 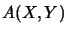 which is a linear subspace of
which is a linear subspace of
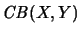 a
a
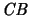 -mapping space.
Note that generally the algebraic identification of
-mapping space.
Note that generally the algebraic identification of
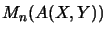 with
with
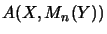 fails to be isometric and that
the norms on
fails to be isometric and that
the norms on
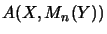 do not generate an
operator space structure for
do not generate an
operator space structure for 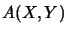 .
.
There is a close relationship between mapping spaces and
tensor products:
The space 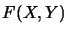 of all finite rank maps
between
of all finite rank maps
between  and
and 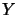 and the algebraic tensor product of
and the algebraic tensor product of 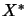 with
with 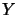 are isomorphic:
are isomorphic:
This identification enables us to transfer norms from one space
to the other one.
To this end, we consider the extension of the mapping
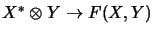 to the completion with respect to an operator space tensor norm
to the completion with respect to an operator space tensor norm
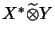 :
:
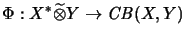
.

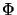 is in general neither injective nor surjective.
As a CB-mapping space one obtains
with the operator space
norm of
is in general neither injective nor surjective.
As a CB-mapping space one obtains
with the operator space
norm of
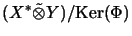
.
We consider now assignments that assign a
mapping space
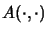 with operator space norm
with operator space norm
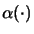 to every pair of
operator spaces. In the Banach space theory
A. Pietsch intensified the notion of mapping spaces to that of
the
operator ideals [Pie78].
Analogously, we consider operator ideals which are
mapping spaces with the
to every pair of
operator spaces. In the Banach space theory
A. Pietsch intensified the notion of mapping spaces to that of
the
operator ideals [Pie78].
Analogously, we consider operator ideals which are
mapping spaces with the
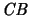 -ideal property [ER94],
i.e , the composition
-ideal property [ER94],
i.e , the composition
is for all operator spaces 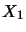 ,
, 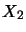 ,
, 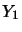 ,
, 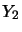 defined and
jointly completely contractive .
defined and
jointly completely contractive .
A
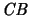 -ideal is called local [EJR98],
if its norm satisfies:
-ideal is called local [EJR98],
if its norm satisfies:
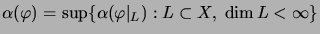
.

Subsections





Next: Completely nuclear mappings
Up: What are operator spaces?
Previous: -extreme points
Contents
Index
Prof. Gerd Wittstock
2001-01-07
![]() which is a linear subspace of
which is a linear subspace of
![]() a
a
![]() -mapping space.
Note that generally the algebraic identification of
-mapping space.
Note that generally the algebraic identification of
![]() with
with
![]() fails to be isometric and that
the norms on
fails to be isometric and that
the norms on
![]() do not generate an
operator space structure for
do not generate an
operator space structure for ![]() .
.
![]() of all finite rank maps
between
of all finite rank maps
between ![]() and
and ![]() and the algebraic tensor product of
and the algebraic tensor product of ![]() with
with ![]() are isomorphic:
are isomorphic:
![]() -ideal is called local [EJR98],
if its norm satisfies:
-ideal is called local [EJR98],
if its norm satisfies: