



Nächste Seite: Archimedisches Axiom
Aufwärts: Konvergenz und Stetigkeit
Vorherige Seite: Konvergenz und Stetigkeit
Inhalt
Im vorigen Abschnitt haben wir eine Intervallschachtelung konstruiert,
mit der wir die Eulersche Zahl 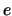 bestimmen.
Das war etwas aufwendig,
aber für diese Zahl lohnt sich die Mühe.
Die Intervallschachtelung hat den Vorteil, daß sie die gesuchte
Zahl nach unten und oben immer genauer abschätzt.
bestimmen.
Das war etwas aufwendig,
aber für diese Zahl lohnt sich die Mühe.
Die Intervallschachtelung hat den Vorteil, daß sie die gesuchte
Zahl nach unten und oben immer genauer abschätzt.
Vielfach hat man zur Bestimmung einer Zahl
- z.B. der Lösung einer Gleichung -
nur eine Folge von approximativen Wert 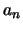 (
(
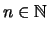 )
zur Verfügung.
)
zur Verfügung.
Die Folge wird am Anfang vielleicht wild schwanken
und sich schließlich mit immer
kleineren Abweichungen einem festen Wert 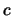 nähern.
nähern.
Man sagt, die Folge 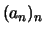 konvergiert gegen den Grenzwert
konvergiert gegen den Grenzwert 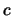 .
.
Wir wollen dieses anschauliche Bild präziser definieren.
Definition 2.1.1
Eine Folge
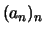
in
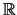
heißt
konvergent gegen einen
Grenzwert
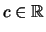
, wenn folgendes gilt:
Zu jedem
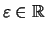 ,
,
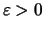 gibt es einen Index
gibt es einen Index
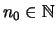 ,
so daß aus
,
so daß aus
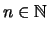 ,
,
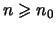 , stets
, stets
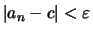 .
.
folgt.
Nicht konvergente Folgen heißen
divergent.
Bemerkung 2.1.2
- Konvergiert eine Folge nicht, so sagt man, sie divergiert.
- Eine Folge, die gegen Null konvergiert, heißt Nullfolge.
- Man sagt, eine Eigenschaft gilt für fast alle
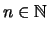 ,
wenn es ein
,
wenn es ein
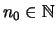 so gibt, daß die Eigenschaft für alle
so gibt, daß die Eigenschaft für alle
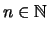 ,
,
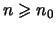 , gilt.
, gilt.
Feststellung 2.1.3 (Eindeutigkeit des Grenzwertes)
Eine Folge 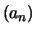 in
in
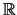 hat höchstens einen Grenzwert.
hat höchstens einen Grenzwert.
D.h., Wenn 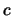 und
und 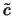 Grenzwerte einer Folge
Grenzwerte einer Folge 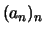 sind, dann ist
sind, dann ist
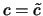 .
.
Bezeichnung 2.1.4 (Grenzwert)
- Wenn die Folge
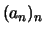 konvergent gegen den (eindeutigen) Grenzwert
konvergent gegen den (eindeutigen) Grenzwert 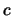 ist,
so bezeichnen wir den Grenzwert mit:
Das obige Symbol besagt, daß die Folge
ist,
so bezeichnen wir den Grenzwert mit:
Das obige Symbol besagt, daß die Folge
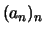 konvergiert.
konvergiert.
- Eine andere praktische Kurzschreibweise ist:
- Bindung:
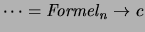 aber
aber
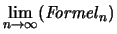 .
.
Die beiden folgenden Konvergenzkriterien
sind oftmals handlicher als die Definition ![[*]](crossref.png) .
Der freiwählbare konstante Faktor
.
Der freiwählbare konstante Faktor 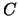 und ,,
und ,,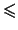 ``
statt des ,,
``
statt des ,,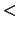 `` erleichtern das Abschätzen.
`` erleichtern das Abschätzen.
Feststellung 2.1.5
Eine Folge
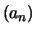
konvergiert genau dann gegen
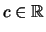
,
wenn es ein
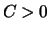
mit der folgenden Eigenschaft gibt:
Für alle
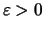 gibt es ein
gibt es ein
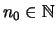 , so daß aus
, so daß aus
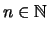 ,
,
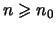 stets
stets
folgt.
Die folgende Formulierung kommt ohne ganz ,,Epsilontik`` aus:
Unterabschnitte




Nächste Seite: Archimedisches Axiom
Aufwärts: Konvergenz und Stetigkeit
Vorherige Seite: Konvergenz und Stetigkeit
Inhalt
Analysis1-A.Lambert
2001-02-09
![]() (
(
![]() )
zur Verfügung.
)
zur Verfügung.
![]() nähern.
nähern.
![]() konvergiert gegen den Grenzwert
konvergiert gegen den Grenzwert ![]() .
.
![]() ,
,
![]() gibt es einen Index
gibt es einen Index
![]() ,
so daß aus
,
so daß aus
![]() ,
,
![]() , stets
, stets
![]() in
in
![]() hat höchstens einen Grenzwert.
hat höchstens einen Grenzwert.![]() und
und ![]() Grenzwerte einer Folge
Grenzwerte einer Folge ![]() sind, dann ist
sind, dann ist
![]() .
.
![[*]](crossref.png) .
Der freiwählbare konstante Faktor
.
Der freiwählbare konstante Faktor ![]() und ,,
und ,,![]() ``
statt des ,,
``
statt des ,,![]() `` erleichtern das Abschätzen.
`` erleichtern das Abschätzen.
![]() gibt es ein
gibt es ein
![]() , so daß aus
, so daß aus
![]() ,
,
![]() stets
stets