Bemerkung.
Wir können leicht Beispiele von divergenten Folgen finden:
![]() ist sicher divergent.
ist sicher divergent.
Konstante Folgen sind konvergent.
Wenn man interessante Beispiele sucht, stößt man auf ein Problem,
daß wir am Beispiel der Folge
![]() aufzeigen wollen.
aufzeigen wollen.
![[*]](crossref.png) aber wir für beliebige
aber wir für beliebige
Man vergleiche dazu aber die Folgerung ![[*]](crossref.png) aus dem Archimedischen Axiom (A).
aus dem Archimedischen Axiom (A).
Anmerkung: Die Definition des Grenzwertes
![[*]](crossref.png) ist nicht nur für
ist nicht nur für
![]() ,
sondern für jeden geordneten Körper
(vgl. Def.
,
sondern für jeden geordneten Körper
(vgl. Def. ![[*]](crossref.png) )
anwendbar.
Die Folge
)
anwendbar.
Die Folge ![]() und der Grenzwert
und der Grenzwert ![]() liegen dann
in diesem geordnetem Körper.
liegen dann
in diesem geordnetem Körper.
Man beachte, daß man in diesem Fall
auch die Vergleichswerte
![]() aus diesem Körper wählen muß.
aus diesem Körper wählen muß.
Das folgende Lemma gilt für jeden geordneten Körper.
Wenn die Folge
![]() konvergiert, dann ist der Grenzwert Null.
konvergiert, dann ist der Grenzwert Null.
Beweisidee: Wenn
![]() dann gilt
dann gilt
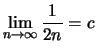 und
und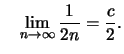
Wir haben die eben benutzten Rechenregeln für Grenzwerte noch nicht bewiesen und zeigen diese Schlußweise direkt mit der Grenzwertdefinition.
Beweis . Es sei
![]() .
.
Zu
![]() existiert ein
existiert ein
![]() , so daß
, so daß
Anmerkung:
![[*]](crossref.png) wir für beliebige
wir für beliebige
(K) und (O) besagen nur, daß
![]() ist ein geordneter Körper ist.
Das reicht nicht aus!
ist ein geordneter Körper ist.
Das reicht nicht aus!
Die Folge
![]() ist genau dann konvergent,
wenn
ist genau dann konvergent,
wenn
![]() unbeschränkt ist.
unbeschränkt ist.
![[*]](crossref.png)
Beweis .
Ist nun
![]() ,
, ![]() so setze man
so setze man
![]() .
Nach der Definition des Grenzwertes gibt es ein
.
Nach der Definition des Grenzwertes gibt es ein
![]() so daß
so daß
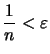
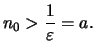
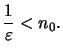
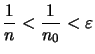
Wir lösen das Problem durch ein weiteres Axiom, das Axiom des Archimedes:
Archimedes von Syrakus (312-287 v. Chr.)