![[*]](crossref.png) als Vergleichwerte
als Vergleichwerte
Inbesondere reicht es, die Grenzwertbedingung ![[*]](crossref.png) nur für die
Werte
nur für die
Werte
![]() , (
, (
![]() ), nachzuprüfen.
), nachzuprüfen.
![[*]](crossref.png) als Vergleichwerte
als Vergleichwerte
Inbesondere reicht es, die Grenzwertbedingung ![[*]](crossref.png) nur für die
Werte
nur für die
Werte
![]() , (
, (
![]() ), nachzuprüfen.
), nachzuprüfen.
Die letzte Festellung ermöglicht induktive Beweise!
Es seien ![]() und
und ![]() Folgen in
Folgen in
![]() . Dann gilt:
. Dann gilt:
Bemerkung:
In ![[*]](crossref.png) . reicht es, daß
. reicht es, daß
![]() für fast alle
für fast alle
![]() gilt
(vgl.
gilt
(vgl. ![[*]](crossref.png) (
(![[*]](crossref.png) ))
))
Beweis (c).
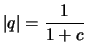 mit
mit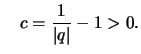
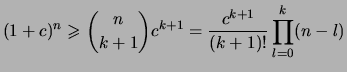
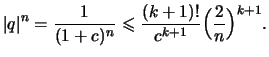
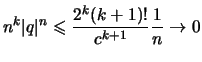 .
.
Beweis (Einsperregel). Da
![]() und
und
![]() , gilt
, gilt
![]() .
Für fast alle
.
Für fast alle
![]() gilt:
gilt:
![[*]](crossref.png)
Es seien ![]() ,
, ![]() Folgen mit
Folgen mit
![]() und
und
![]() . Dann ist
. Dann ist
Anmerkung: Für keine der Aussagen gilt die Umkehrung.
Beweis (Rechenregeln für Grenzwerte). Wir führen mit Hilfe von
![[*]](crossref.png) die Behauptungen auf die Regeln
die Behauptungen auf die Regeln
![[*]](crossref.png) für Nullfolgen
zurück:
für Nullfolgen
zurück:
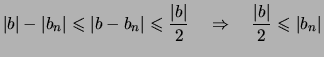
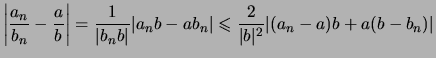 .
.
Beweis .
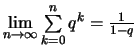 .
.
Anmerkung: Aus ![]() folgt auch nur
folgt auch nur
![]() .
.
Anmerkung
![[*]](crossref.png) der harmonischen Reihe zeigt, daß die Umkehrung nicht gilt.
der harmonischen Reihe zeigt, daß die Umkehrung nicht gilt.
Zur Vorbereitung des Beweises überlegen wir uns, was heißt es,
daß eine Folge ![]() keine Nullfolge ist:
keine Nullfolge ist:
Annahme, die Folge ![]() konvergiert nicht gegen
konvergiert nicht gegen ![]() .
Dann gibt es ein
.
Dann gibt es ein
![]() und eine streng monoton wachsende Folge
und eine streng monoton wachsende Folge
![]() in
in
![]() , so daß
, so daß
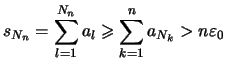 für
für
Das folgende Korollar werden wir im Abschnitt Cauchy-Folgen
wesentlich verschärfen (vgl. ![[*]](crossref.png) ).
Dabei werden wir eine ähnliche Beweisidee verwenden.
).
Dabei werden wir eine ähnliche Beweisidee verwenden.
Beweis . Ohne Einschränkung sei ![]() monoton wachsend und nach oben
beschränkt.
Man bilde die Folge
monoton wachsend und nach oben
beschränkt.
Man bilde die Folge
![]() ,
,
![]() und die
Partialsummen
und die
Partialsummen
![]() .
Da die Folge
.
Da die Folge ![]() beschränkt ist, folgt
beschränkt ist, folgt
![]() .
.