



Nächste Seite: Grenzwerte von Funktionen und
Aufwärts: Vollständigkeit der reellen Zahlen
Vorherige Seite: Monotone Folgen
Inhalt
Feststellung 2.2.13 (Approximation der n-ten Wurzel)
Es seien
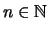
und
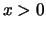
.
Wir erhalten eine monoton fallende Folge
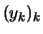
positiver Zahlen durch die Vorschrift:
| |
Startwert: |
|
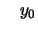 mit mit
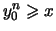 , , |
|
| |
Rekursion: |
|
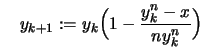 |
|
mit folgenden Eigenschaften:
Für den Grenzwert
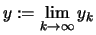
gilt
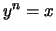
.
Bemerkung: Als Startwert kann man z.B.
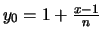 wählen.
Dann ist
wählen.
Dann ist
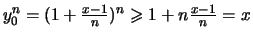 .
.
Beweis . Die Abschätzungen folgen durch
Induktion nach 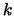 .
.
-
Die beiden ersten Aussagen sind klar nach Definition.
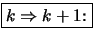
- Da
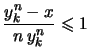 folgt nach Bernoulli (
folgt nach Bernoulli (![[*]](crossref.png) ):
):
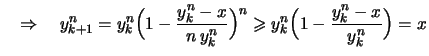 .
.
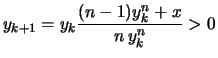 .
.
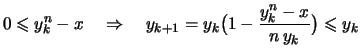 .
.
Also existiert
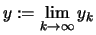 .
Aus der Rekursionsformel folgt:
.
Aus der Rekursionsformel folgt:
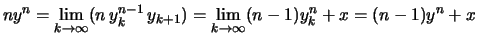 .
.
Folglich ist 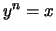 .
.
Satz 2.2.14
Zu
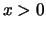
und
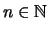
existiert eine eindeutig bestimmte reelle Zahl
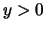
mit
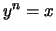
.
Bezeichnung. Die eindeutig bestimmte Zahl 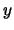 aus vorigem Satz heißt die
aus vorigem Satz heißt die
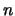 -te Wurzel aus
-te Wurzel aus 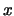 . Bezeichnung:
. Bezeichnung:
![$ y=\sqrt[\uproot{2}n]{x}$](img1028.png) Man setzt
Man setzt
![$ \sqrt[\uproot{2}n]{0} :=0 $](img1029.png) .
.
Beweis .
- Eindeutigkeit:
- Es seien
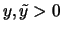 .
Wenn
.
Wenn
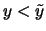 , dann ist
, dann ist
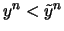 .
Aus
.
Aus
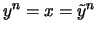 folgt also
folgt also
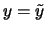 .
.
- Existenz:
- Die Existenz der n-ten Wurzel folgt aus
der Festellung
![[*]](crossref.png) .
.
Satz 2.2.17 (Bernoullische Ungleichung für die Wurzel)
Für 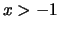 ,
,
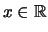 , und
, und
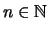 gilt:
gilt:
![$\displaystyle 1 +\frac{x}{n(1+x)}
\leqslant \sqrt[\uproot{2}n]{1+x} \leqslant 1 + \frac{x}{n}$](img1043.png) .
.
Beweis . Wir setzen
![$\displaystyle \sqrt[\uproot{2}n]{1+x} = 1+a$](img1044.png) .
.
Dann ist 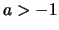 . Nach Bernoulli (
. Nach Bernoulli (![[*]](crossref.png) ) folgt
) folgt
Wenden wir die soeben gezeigt Ungleichung an, so folgt:
![$\displaystyle \sqrt[\uproot{2}n]{1+x} = \frac{1}{ \sqrt[\uproot{2}n]{1-\frac{x}{1+x}}}
\geqslant \frac{1}{1-\frac{x}{n(1+x)}} \geqslant 1 + \frac{x}{n(1+x)}$](img1048.png) .
.
Beweis . Der Fall 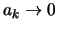 ist klar.
Wenn der Grenzwert
ist klar.
Wenn der Grenzwert 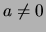 ,
so gibt es ein
,
so gibt es ein
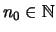 so daß
so daß
Die Behauptung folgt nun aus der Bernoullischen Ungleichung:
![$\displaystyle \sqrt[\uproot{2}n]{a}\Bigl(1+ \frac{a_k-a}{ka_k} \Bigr)
\leqslan...
...\frac{a_k-a}{a}}
\leqslant \sqrt[\uproot{2}n]{a}\Bigl(1+ \frac{a_k-a}{ka}\Bigr)$](img1053.png) .
.
Feststellung 2.2.19
Es sei
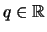
,
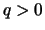
. Dann ist
![$\displaystyle \lim\limits_{n\to\infty}\sqrt[\uproot{2}n]{q} = 1$](img1055.png) .
.
Die Folge
![$\displaystyle (\sqrt[\uproot{2}n]{q})_n$](img1056.png) ist
ist
Bemerkung:
Die Konvergenz
![$ \sqrt[\uproot{2}n]{q}\to 1 $](img1058.png) folgt aus der Bernoullischen
Ungleichung:
Für
folgt aus der Bernoullischen
Ungleichung:
Für 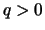 gilt:
gilt:
![$\displaystyle 1 +\frac{1}{n}\Bigl(1-\frac{1}{q}\Bigr)
\leqslant\sqrt[\uproot{2}n]{q}\leqslant 1 + \frac{1}{n}(q-1)$](img1059.png) .
.
Beispiel.
![$\displaystyle 1.05 \leqslant \sqrt[\uproot{2}10]{2} \approx 1.0718 \leqslant 1.1$](img1060.png) , , |
|
![$\displaystyle 1.000999 \leqslant \sqrt[\uproot{2}1000]{1000} \approx 1.0069 \leqslant 1.999\,$](img1061.png) . . |
|
Beweis . Für 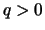 setze man
setze man
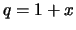 mit
mit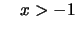
und wende die Bernoullische Ungleichung
![[*]](crossref.png) an:
an:
![$\displaystyle 1 +\frac{x}{n(1+x)}
\leqslant \sqrt[\uproot{2}n]{1+x} \leqslant 1 + \frac{x}{n}$](img1043.png) .
.
Also ist
![$ \lim\limits_{n\to\infty}\sqrt[\uproot{2}n]{1+x} = 1 $](img1064.png) .
.
Im Falle 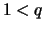 ist
ist
![$ \sqrt[\uproot{2}n]{q} > 1 $](img1066.png) und aus
und aus
folgt die strenge Monotonie der Folge:
![$ \sqrt[\uproot{2}n+1]{q} < \sqrt[\uproot{2}n]{q} $](img1068.png) .
.
Im Falle 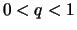 sind die Kehrwerte
sind die Kehrwerte
![$ \sqrt[\uproot{2}n]{\frac{1}{q}} $](img1070.png) streng monoton fallend.
streng monoton fallend.
Feststellung 2.2.20
Die Folge
![$ \sqrt[\leftroot{0}\uproot{2}n]{n}$](img1071.png)
, (
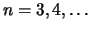
), ist
streng monoton fallend und es ist
Bemerkung. Die Behauptungen folgen aus der Abschätzung
Beweis . Nach Lemma ![[*]](crossref.png) gilt
gilt
Wir setzen
![$ a_n = \sqrt[\uproot{2}n]{n} -1 $](img1078.png) .
.
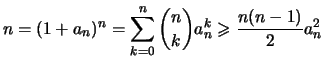 .
.
Also ist
![$\displaystyle \sqrt[\uproot{2}n]{n}= 1+ a_n \leqslant 1 + \sqrt{\frac{2}{n-1}}$](img1080.png) .
.




Nächste Seite: Grenzwerte von Funktionen und
Aufwärts: Vollständigkeit der reellen Zahlen
Vorherige Seite: Monotone Folgen
Inhalt
Analysis1-A.Lambert
2001-02-09
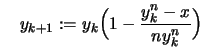
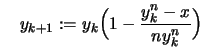
![]() wählen.
Dann ist
wählen.
Dann ist
![]() .
.
![]() .
.
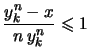 folgt nach Bernoulli (
folgt nach Bernoulli (![[*]](crossref.png) ):
):
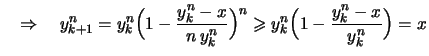 .
.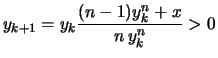 .
.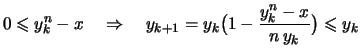 .
.![]() aus vorigem Satz heißt die
aus vorigem Satz heißt die
![]() -te Wurzel aus
-te Wurzel aus ![]() . Bezeichnung:
. Bezeichnung:
![]() Man setzt
Man setzt
![]() .
.
![[*]](crossref.png) .
.
![]() ,
,
![]() :
:
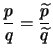 ,
dann ist
,
dann ist
![[*]](crossref.png) ) folgt
) folgt
![$\displaystyle \sqrt[\uproot{2}n]{1+x} = \frac{1}{ \sqrt[\uproot{2}n]{1-\frac{x}{1+x}}}
\geqslant \frac{1}{1-\frac{x}{n(1+x)}} \geqslant 1 + \frac{x}{n(1+x)}$](img1048.png) .
.![]() ist klar.
Wenn der Grenzwert
ist klar.
Wenn der Grenzwert ![]() ,
so gibt es ein
,
so gibt es ein
![]() so daß
so daß
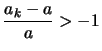 für
für
![$\displaystyle \sqrt[\uproot{2}n]{a}\Bigl(1+ \frac{a_k-a}{ka_k} \Bigr)
\leqslan...
...\frac{a_k-a}{a}}
\leqslant \sqrt[\uproot{2}n]{a}\Bigl(1+ \frac{a_k-a}{ka}\Bigr)$](img1053.png) .
.
![]() folgt aus der Bernoullischen
Ungleichung:
Für
folgt aus der Bernoullischen
Ungleichung:
Für ![]() gilt:
gilt:
![$\displaystyle 1 +\frac{1}{n}\Bigl(1-\frac{1}{q}\Bigr)
\leqslant\sqrt[\uproot{2}n]{q}\leqslant 1 + \frac{1}{n}(q-1)$](img1059.png) .
.![]() setze man
setze man
![[*]](crossref.png) an:
an:
![]() ist
ist
![]() und aus
und aus
![]() sind die Kehrwerte
sind die Kehrwerte
![]() streng monoton fallend.
streng monoton fallend.
![$\displaystyle 1+\frac{1}{n} <
\sqrt[\uproot{2}n]{n} < 1 + \sqrt{\frac{2}{n-1}}$](img1074.png) für
für
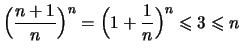 für
für
![$\displaystyle \Rightarrow\quad 1+\frac{1}{n} < \sqrt[\uproot{2}n]{n}
$](img1076.png)
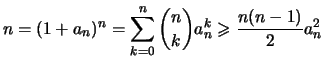 .
.![$\displaystyle \sqrt[\uproot{2}n]{n}= 1+ a_n \leqslant 1 + \sqrt{\frac{2}{n-1}}$](img1080.png) .
.