Es sei ![]() eine Folge mit nichtnegativen Gliedern.
Wenn die Folge der Partialsummen
eine Folge mit nichtnegativen Gliedern.
Wenn die Folge der Partialsummen
![]() nach oben
beschränkt ist, dann existiert der Grenzwert
nach oben
beschränkt ist, dann existiert der Grenzwert
![]() .
.
Jedem Satz über monotone Folgen entspricht ein Satz über Reihen mit nichtnegativen Summanden und umgekehrt.
Es sei ![]() eine Folge mit nichtnegativen Gliedern.
Wenn die Folge der Partialsummen
eine Folge mit nichtnegativen Gliedern.
Wenn die Folge der Partialsummen
![]() nach oben
beschränkt ist, dann existiert der Grenzwert
nach oben
beschränkt ist, dann existiert der Grenzwert
![]() .
.
Beweis . Wir zeigen, daß die Folge ![]() eine Cauchy-Folge ist.
eine Cauchy-Folge ist.
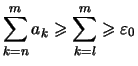 .
.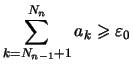 für
für
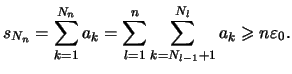
Beweis . Die Folge ![]() sei monoton wachsend und nach oben beschränkt.
Die Folge
sei monoton wachsend und nach oben beschränkt.
Die Folge
![]() , (
, (
![]() ), ist nichtnegativ
und folglich ist nach Satz
), ist nichtnegativ
und folglich ist nach Satz ![[*]](crossref.png) die Folge der
Partialsummen
die Folge der
Partialsummen
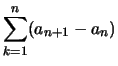 konvergent.
konvergent.
Dann gilt:
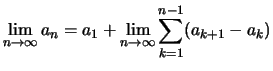 .
.
Für monoton fallende, nach unten beschränkte Folgen ![]() existiert
existiert
![]() und folglich
nach den Rechenregeln
und folglich
nach den Rechenregeln
![[*]](crossref.png) auch
auch