Gegeben seien:
- eine nichtleere Menge
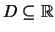 und ein
und ein
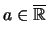 ,
so daß es eine Folge
,
so daß es eine Folge 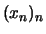 in
in 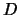 gibt,
die gegen
gibt,
die gegen  konvergiert,
konvergiert,
- eine Funktion
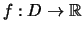 und ein
und ein
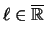 .
.
Die Funktion ![]() konvergiert gegen
konvergiert gegen ![]() für
für
![]() , falls für jede Folge
, falls für jede Folge ![]() in
in
![]() aus
aus
![]() stets
stets
![]() folgt.
folgt.
Eng verwandt mit dem Begriff der Stetigkeit ist der Grenzwertbegriff für Funktionen auf allgemeinen Definitionsbereichen:
Gegeben seien:
Die Funktion ![]() konvergiert gegen
konvergiert gegen ![]() für
für
![]() , falls für jede Folge
, falls für jede Folge ![]() in
in
![]() aus
aus
![]() stets
stets
![]() folgt.
folgt.
Bezeichnung.
Wir schreiben für obige Definition:
![]() oder
oder
![]() für
für ![]() .
.
Gegeben seien:
Die Funktion ![]() konvergiert gegen
konvergiert gegen ![]() für
für
![]() , falls für jede Folge
, falls für jede Folge ![]() in
in
![]() aus
aus
![]() stets
stets
![]() folgt.
folgt.
Ist ![]() , so kann bei diesem Grenzwertbegriff sehrwohl der Grenzwert
für
, so kann bei diesem Grenzwertbegriff sehrwohl der Grenzwert
für ![]() existieren und
existieren und ![]() dennoch unstetig in
dennoch unstetig in ![]() sein!
sein!
Bezeichnung. Wenn es eine Folge ![]() in
in
![]() gibt,
die gegen
gibt,
die gegen ![]() konvergiert
und der Grenzwert der Einschränkung
konvergiert
und der Grenzwert der Einschränkung
![]() im Punkte
im Punkte ![]() existiert, dann bezeichnet man diesen Grenzwert mit:
existiert, dann bezeichnet man diesen Grenzwert mit:
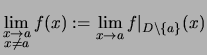
Gegeben seien:
Der Beweis des Satzes ist offensichtlich (vgl. Lemma ![[*]](crossref.png) )
)